题目内容
3.已知函数f(x)=sin(2x+φ)($0<ϕ<\frac{π}{2}$),且$f(0)=\frac{1}{2}$.(Ⅰ)求函数y=f(x)的最小正周期T及φ的值;
(Ⅱ)当x∈[0,$\frac{π}{2}$]时,求函数y=f(x)的最小值.
分析 (Ⅰ)根据最小正周期的定义即可求出,再根据$f(0)=\frac{1}{2}$,即可求出φ=$\frac{π}{6}$,
(Ⅱ)根据正弦函数的性质即可求出.
解答 解:(Ⅰ)$T=\frac{2π}{2}=π$,
∵f(0)=sinφ=$\frac{1}{2}$,$0<ϕ<\frac{π}{2}$,
∴φ=$\frac{π}{6}$,
(Ⅱ)由(1)可得f(x)=sin(2x+$\frac{π}{6}$),
∵x∈[0,$\frac{π}{2}$],
∴2x+$\frac{π}{6}$∈[$\frac{π}{6}$,$\frac{7π}{6}$],
∴函数y=f(x)的最小值为-$\frac{1}{2}$
点评 本题考查了三角函数的图象和性质,属于基础题.

练习册系列答案
相关题目
14.设向量$\overrightarrow{a}$,$\overrightarrow{b}$的模分别为2和3,且夹角为60°,则|$\overrightarrow{a}$+$\overrightarrow{b}$|等于( )
| A. | $\sqrt{13}$ | B. | 13 | C. | $\sqrt{19}$ | D. | 19 |
11.函数y=a|sinx|+2(a>0)的单调递增区间是( )
| A. | (-$\frac{π}{2}$,$\frac{π}{2}$) | B. | (-π,-$\frac{π}{2}$) | C. | ($\frac{π}{2}$,π) | D. | ($\frac{3π}{2}$,2π) |
15.直线x+2y-5+$\sqrt{15}$=0被圆x2+y2-2x-4y=0截得的弦长为( )
| A. | 1 | B. | 2$\sqrt{2}$ | C. | $\sqrt{2}$ | D. | 2 |
9.如图,已知⊙O的半径为5mm,弦AB=8mm,则圆心O到AB的距离是( )
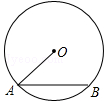

| A. | 1mm | B. | 2mmm | C. | 3mm | D. | 4mm |