题目内容
15.直线x+2y-5+$\sqrt{15}$=0被圆x2+y2-2x-4y=0截得的弦长为( )| A. | 1 | B. | 2$\sqrt{2}$ | C. | $\sqrt{2}$ | D. | 2 |
分析 化圆的方程为标准方程,求出圆的圆心坐标和半径,由点到直线距离公式求出圆心到直线的距离,利用勾股定理求出半弦长,则弦长可求.
解答 解:由x2+y2-2x-4y=0,得(x-1)2+(y-2)2=5,
所以圆的圆心坐标是C(1,2),半径r=$\sqrt{5}$.
圆心C到直线x+2y-5+$\sqrt{15}$=0的距离为d=$\frac{|1+4-5+\sqrt{15}|}{\sqrt{1+4}}$=$\sqrt{3}$.
所以直线直线x+2y-5+$\sqrt{15}$=0=0被圆x2+y2-2x-4y=0截得的弦长为2$\sqrt{5-3}$=2$\sqrt{2}$.
故选B.
点评 本题考查了直线与圆的位置关系,考查了弦心距、圆的半径及半弦长之间的关系,是基础题.

练习册系列答案
相关题目
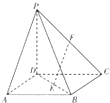 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,PD⊥平面ABCD,AD⊥BD,AD=BD=2,E为BD的中点,F为PC的中点.
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,PD⊥平面ABCD,AD⊥BD,AD=BD=2,E为BD的中点,F为PC的中点.