Question

15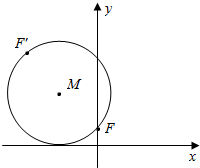．如图所示，已知动圆M过定点F（0，1）且与x轴相切，点F关于圆心M的对称点为F′，动点F′的轨迹为C
（1）求曲线C的方程；
（2）点P在直线1：y=x-2上，过P作曲线C的两条切线，切点为A、B，求证：直线AB恒过定点Q；
（3）若直线PQ与曲线C交于M、N两点，证明：|PM|•|QN|=|QM|•|PN|

Answer 1

分析 （1）设F′（x，y），则可M（$\frac{x}{2}$，$\frac{y+1}{2}$），圆M的直径为|FF′|=$\sqrt{{x}^{2}+（y-1）^{2}}$，利用动圆M与x轴相切，即可求得曲线C的方程；
（2）先设出切点坐标A（x₁，y₁），B（x₂，y₂），利用导数的几何意义求以A、B为切点的切线方程，再设出P（x₀，x₀-2），代入两条切线方程，得（$\frac{1}{2}$x₁-1）x₀+2-y₁=0．同理，（$\frac{1}{2}$x₂-1）x₀+2-y₂=0．故直线AB的方程为（$\frac{1}{2}$x-1）x₀+2-y=0，过定点（2，2）
（3）先写出直线PQ的方程，代入抛物线方程，得关于x的一元二次方程，为利用韦达定理准备条件，再设M（x₃，y₃），N（x₄，y₄），2x₃x₄-（1+x₀）（x₃+x₄）+2x₀=0，最后利用韦达定理将x₃+x₄和x₃x₄代入即可得证．

解答 （1）解：设动点F′（x，y），则
因为点F（0，1）在圆M上，且点F关于圆心M的对称点为F′，
所以M（$\frac{x}{2}$，$\frac{y+1}{2}$），
且圆M的直径为|FF′|=$\sqrt{{x}^{2}+（y-1）^{2}}$．
由题意，动圆M与x轴相切，
所以$\frac{|y+1|}{2}$=$\frac{1}{2}$$\sqrt{{x}^{2}+（y-1）^{2}}$，
两边平方整理得：x²=4y，
所以曲线C的方程x²=4y．
（2）证明：设A（x₁，y₁），B（x₂，y₂），P（x₀，x₀-1），
由x²=4y，得y′=$\frac{1}{2}$x，x=x₁，y′=$\frac{1}{2}$x₁，
抛物线C在点A处的切线方程为y-y₁=$\frac{1}{2}$x₁（x-x₁），即y=$\frac{1}{2}$x₁x-y₁．
而A点处的切线过点P（x₀，x₀-2），所以x₀-2=$\frac{1}{2}$x₁x₀-y₁，
即（$\frac{1}{2}$x₁-1）x₀+2-y₁=0．同理，（$\frac{1}{2}$x₂-1）x₀+2-y₂=0．
可见，点A、B在直线（$\frac{1}{2}$x-1）x₀+2-y=0上．令$\frac{1}{2}$x-1=0，2-y=0，解得x=y=2，
所以，直线AB过定点Q（2，2）；
（3）解：设P（x₀，x₀-2），M（x₃，y₃），N（x₄，y₄），
直线PQ的方程为y=$\frac{（{x}_{0}-2）-2}{{x}_{0}-2}$（x-2）+2，即y=$\frac{{x}_{0}-4}{{x}_{0}-2}$x+$\frac{4}{{x}_{0}-2}$
代入x²=4y，消去y，得x²-4×$\frac{{x}_{0}-4}{{x}_{0}-2}$x-4×$\frac{4}{{x}_{0}-2}$=0．
由韦达定理，x₃+x₄=4×$\frac{{x}_{0}-4}{{x}_{0}-2}$，x₃x₄=-4×$\frac{4}{{x}_{0}-2}$．
因为$\frac{|PM|}{|PN|}$=$\frac{|QM|}{|QN|}$，可得$\frac{{x}_{3}-{x}_{0}}{{x}_{4}-{x}_{0}}$=$\frac{1-{x}_{3}}{{x}_{4}-1}$
所以2x₃x₄-（x₃+x₄）-x₀（x₃+x₄）+2x₀=0（*）
代入方程（*）的左边，得（*）的左边=2×（-4×$\frac{4}{{x}_{0}-2}$）-（4×$\frac{{x}_{0}-4}{{x}_{0}-2}$）-x₀（4×$\frac{{x}_{0}-4}{{x}_{0}-2}$）+2x₀=0．
因而有|PM|•|QN|=|QM|•|PN|．

点评 本题考查轨迹方程的求解，考查直线的斜率，考查直线与抛物线的位置关系，考查抛物线的切线方程，考查学生分析解决问题的能力，属于难题．