题目内容
20．设函数f（x）=x2+（a-2）x-1在区间（-∞，2]是减函数，则实数a的最大值为-2．分析 利用二次函数的对称轴与函数的单调性求解即可．
解答 解：函数f（x）=x2+（a-2）x-1的开口向上，对称轴为：x=$\frac{2-a}{2}$，
函数f（x）=x2+（a-2）x-1在区间（-∞，2]是减函数，
可得$\frac{2-a}{2}≥2$
解得a≤-2．
实数a的最大值为：-2．
故答案为：-2．
点评 本题考查二次函数的性质的应用，表达式的最值的求法，考查计算能力．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
8．已知f（x+y）=f（x）+f（y）对任意实数x，y都成立，则函数f（x）是（ ）
| A． | 奇函数 | B． | 偶函数 | ||
| C． | 既是奇函数又是偶函数 | D． | 不能判断奇偶性 |
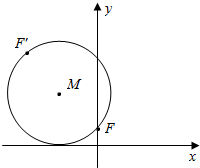如图所示，已知动圆M过定点F（0，1）且与x轴相切，点F关于圆心M的对称点为F′，动点F′的轨迹为C