��Ŀ����
2�� ij��������Ϊ�˽Ȿ��������ѧ������������������ȡ��100��ѧ�����е��飮�����Ǹ��ݵ��������Ƶ�ѧ��ÿ������ʱ���Ƶ�ʷֲ�ֱ��ͼ����ÿ������ʱ�䲻����40���ӵ�ѧ����Ϊ�������ԡ���
ij��������Ϊ�˽Ȿ��������ѧ������������������ȡ��100��ѧ�����е��飮�����Ǹ��ݵ��������Ƶ�ѧ��ÿ������ʱ���Ƶ�ʷֲ�ֱ��ͼ����ÿ������ʱ�䲻����40���ӵ�ѧ����Ϊ�������ԡ�����1��������֪������������2��2�����������ݴ��������Ƿ���Ϊ�������ԡ����Ա��йأ�
| �������� | ������ | �ϼ� | |
| �� | |||
| Ů | 10 | 55 | |
| �ϼ� |
����X2=$\frac{n��{n}_{11}{n}_{22}-{n}_{12}{n}_{21}��^{2}}{��{n}_{11}+{n}_{12}����{n}_{21}+{n}_{22}����{n}_{11}+{n}_{21}����{n}_{12}+{n}_{22}��}$��
| P��X2��k�� | 0.05 | 0.01 |
| k | 3.841 | 6.635 |
���� ��1������������Ƶ�ʷֲ�ֱ��ͼ�ó������г����������ٴ��빫ʽ����ó�K2����3.841�Ƚϼ��ɵó����ۣ�
��2����Ƶ�ʷֲ�ֱ��ͼ֪�鵽�������ԡ���Ƶ��Ϊ0.25����Ƶ����Ϊ���ʣ����ӹ����г�ȡһ���������ԡ��ĸ���Ϊ$\frac{1}{4}$���ɵý��ۣ�
��� �⣺��1����Ƶ�ʷֲ�ֱ��ͼ��֪���ڳ�ȡ��100���У��������ԡ���25�ˣ��Ӷ�2��2���������£�
| �������� | ������ | �ϼ� | |
| �� | 30 | 15 | 45 |
| Ů | 45 | 10 | 55 |
| �ϼ� | 75 | 25 | 100 |
��Ϊ3.030��3.841������û��������Ϊ�������ԡ����Ա��йأ�
��2����Ƶ�ʷֲ�ֱ��ͼ֪�鵽�������ԡ���Ƶ��Ϊ0.25����Ƶ����Ϊ���ʣ����ӹ����г�ȡһ���������ԡ��ĸ���Ϊ$\frac{1}{4}$����$P��X=2��=\frac{9}{64}$��
���� ������Ҫ����Ƶ�ʷֲ�ֱ��ͼ��Ӧ�á������Լ��顢���ʼ��㣬����������ѧ֪ʶ���ʵ���������������е��⣮

��ϰ��ϵ�д�
�����Ŀ
10������2011����ÿ��ٰ�һ�����νڣ���2016���Ѿٰ������죬���β���ͳ����ÿ�����ν��ڼ䣬�����˲�������ο͵����ģ��⽫������ƽ����ĵ�����ҵ�ķ�չ���ֽ�ǰ������ν��ڼ�����ο͵����ĵ�����ͳ�����±���
��1����y����x�����Իع鷽��$\stackrel{��}{y}$=$\stackrel{��}{b}$x+$\stackrel{��}{a}$��
$\stackrel{��}{b}$=$\frac{\sum_{i=1}^{n}��{x}_{i}-\overline{x}����{y}_{i}-\overline{y}��}{\sum_{i=1}^{n}��{x}_{i}-\overline{x}��^{2}}$
��2�����ã�1���е����Իع鷽�̣�Ԥ��17���7�����ν��ڼ�����ο͵����ĵ�������
| ��� | 11�� | 12�� | 13�� | 14�� | 15�� |
| ���νڽ���x | 1 | 2 | 3 | 4 | 5 |
| ����ο�����y����λ��ʮ�� | 0.6 | 0.8 | 0.9 | 1.2 | 1.5 |
$\stackrel{��}{b}$=$\frac{\sum_{i=1}^{n}��{x}_{i}-\overline{x}����{y}_{i}-\overline{y}��}{\sum_{i=1}^{n}��{x}_{i}-\overline{x}��^{2}}$
��2�����ã�1���е����Իع鷽�̣�Ԥ��17���7�����ν��ڼ�����ο͵����ĵ�������
7����ͬһ����ϵ�У�������y=2sin3x��Ϊ����y'=sinx'�������任�ǣ�������
| A�� | $\left\{{\begin{array}{l}{x=3x'}\\{y=\frac{1}{2}y'}\end{array}}\right.$ | B�� | $\left\{{\begin{array}{l}{x'=3x}\\{y'=\frac{1}{2}y}\end{array}}\right.$ | C�� | $\left\{{\begin{array}{l}{x=3x'}\\{y=2y'}\end{array}}\right.$ | D�� | $\left\{{\begin{array}{l}{x'=3x}\\{y'=2y}\end{array}}\right.$ |
14��������ʵ��������f��x��=2cos��x��x��$[{0��\frac{2��}{3}}]$���Ǽ�������������Сֵ1����ô�ص�ֵ�����ǣ�������
| A�� | 2 | B�� | $\frac{1}{2}$ | C�� | $\frac{1}{3}$ | D�� | 3 |
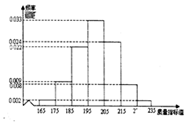 ��ij��ҵ��ij�ֲ�Ʒ�г�ȡ500����������Щ��Ʒ��һ������ָ��ֵ���ɲ������������Ƶ�ʷֲ�ֱ��ͼ��
��ij��ҵ��ij�ֲ�Ʒ�г�ȡ500����������Щ��Ʒ��һ������ָ��ֵ���ɲ������������Ƶ�ʷֲ�ֱ��ͼ��