题目内容
12．运行如图所示的程序框图，则输出的结果是（ ）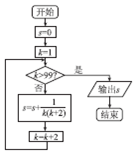
| A． | $\frac{49}{99}$ | B． | $\frac{50}{101}$ | C． | $\frac{51}{103}$ | D． | $\frac{1}{2}$ |
分析 程序框图累计算$\frac{1}{k（k+2）}$=$\frac{1}{2}$（$\frac{1}{k}$-$\frac{1}{k+2}$）各项的和，即s=$\frac{1}{2}$[（1-$\frac{1}{3}$）+（$\frac{1}{3}$-$\frac{1}{5}$）+…+（$\frac{1}{99}$-$\frac{1}{101}$）]，
根据判断框，即可得出结论．
解答 解：程序框图累计算$\frac{1}{k（k+2）}$=$\frac{1}{2}$（$\frac{1}{k}$-$\frac{1}{k+2}$）各项的和，
即s=$\frac{1}{2}$[（1-$\frac{1}{3}$）+（$\frac{1}{3}$-$\frac{1}{5}$）+…+（$\frac{1}{99}$-$\frac{1}{101}$）]，
判断框为k＞99时，输出的结果为$\frac{50}{101}$，
故选B．
点评 算法是新课程中的新增加的内容，也必然是新高考中的一个热点，应高度重视．程序填空也是重要的考试题型，这种题考试的重点有：①分支的条件②循环的条件③变量的赋值④变量的输出．其中前两点考试的概率更大．此种题型的易忽略点是：不能准确理解流程图的含义而导致错误．
练习册系列答案
相关题目
3．要得到函数y=sin（3x-$\frac{π}{4}$）的图象，只需将函数y=cos3x的图象（ ）
| A． | 向右平移$\frac{π}{4}$个单位 | B． | 向左平移$\frac{π}{4}$个单位 | ||
| C． | 向右平移$\frac{3π}{4}$个单位 | D． | 向左平移$\frac{3π}{4}$个单位 |
20．
为了摸清整个江门大道的交通状况，工作人员随机选取20处路段，在给定的测试时间内记录到机动车的通行数量情况如下（单位：辆）：
147 161 170 180 163 172 178 167 191 182
181 173 174 165 158 154 159 189 168 169
（Ⅰ）完成如下频数分布表，并作频率分布直方图；
（Ⅱ）现用分层抽样的方法从通行数量区间为[165，175）、[175，185）及[185，195）的路段中取出7处加以优化，再从这7处中随机选2处安装智能交通信号灯，设所取出的7处中，通行数量区间为[165，175）路段安装智能交通信号灯的数量为随机变量X（单位：盏），试求随机变量X的分布列与数学期望E（X）．
为了摸清整个江门大道的交通状况，工作人员随机选取20处路段，在给定的测试时间内记录到机动车的通行数量情况如下（单位：辆）：147 161 170 180 163 172 178 167 191 182
181 173 174 165 158 154 159 189 168 169
（Ⅰ）完成如下频数分布表，并作频率分布直方图；
| 通行数量区间 | [145，155） | [155，165） | [165，175） | [175，185） | [185，195） |
| 频数 |
7．设函数f（x）=x2-2x-3，若从区间[-2，4]上任取一个实数x0，则所选取的实数x0满足f（x0）≤0的概率为（ ）
| A． | $\frac{2}{3}$ | B． | $\frac{1}{2}$ | C． | $\frac{1}{3}$ | D． | $\frac{1}{4}$ |
17．已知集合A={x|-1＜x＜3}，B={x|x＜a}，若A∩B=A，则实数a的取值范围是（ ）
| A． | a＞3 | B． | a≥3 | C． | a≥-1 | D． | a＞-1 |
19．设全集U=A∪B={1，2，3，4，5}，A∩（∁UB）={1，2}，则集合B=（ ）
| A． | {2，4，5} | B． | {3，4，5} | C． | {4，5} | D． | （2，4） |