题目内容
10.设函数f(x)=x2eax,a>0.(1)证明:函数y=f(x)在(0,+∞)上为增函数;
(2)若方程f(x)-1=0有且只有两个不同的实数根,求实数a的值.
分析 (1)求导,由x∈(0,+∞)则f′(x)>0,则函数y=f(x)在(0,+∞)上为增函数;
(2)求导,f′(x)=0,根据函数的单调性即可求得f(x)极大值,由f(x)=1有且只有两个不同的实数根,即$\frac{4}{{a}^{2}{e}^{2}}$=1,即可求得实数a的值.
解答 解:(1)证明:f(x)的定义域R,求导,f′(x)=2xeax+ax2eax=xeax(ax+2),
当x∈(0,+∞)时,a>0,则eax>0,则xeax(ax+2)>0,
则f′(x)>0,
∴函数y=f(x)在(0,+∞)上为增函数;
(2)令f′(x)=0,记得x=-$\frac{2}{a}$或x=0,
| x | (-∞,-$\frac{2}{a}$) | $\frac{2}{a}$ | ($\frac{2}{a}$,0) | 0 | (0,+∞) |
| f′(x) | + | 0 | - | 0 | + |
| f(x) | 递增 | 极大值 | 递减 | 极小值 | 递增 |
当x=0时,函数有极小值f(0)=0,
当x<0时,f(x)>0,x→-∞时,f(x)→0,x→+∞时,f(x)→+∞,
由f(x)-1=0,即f(x)=1有且只有两个不同的实数根,
即$\frac{4}{{a}^{2}{e}^{2}}$=1,解得:a=$\frac{2}{e}$,(负根舍去)
实数a的值$\frac{2}{e}$.
点评 本题考查导数的综合应用,考查利用导数与函数单调性与极值关系,考查计算能力,属于中档题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
20.已知集合M={x|x2-4<0},N={x|1≤2x≤8,x∈Z},则N∩M=( )
| A. | [0,2) | B. | {0,1} | C. | {0,1,2} | D. | {0,1,3} |
2.如图所示是一个组合几何体的三视图,则该几何体的体积为( )
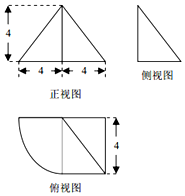

| A. | $\frac{16}{3}$π | B. | $\frac{64}{3}$ | C. | $\frac{16π+64}{3}$ | D. | 16π+64 |