题目内容
定义:如果函数 在区间
在区间 上存在
上存在 ,满足
,满足 则称函数
则称函数 在区间
在区间 上的一个双中值函数,已知函数
上的一个双中值函数,已知函数 是区间
是区间 上的双中值函数,则实数
上的双中值函数,则实数 的取值范围是 ( )
的取值范围是 ( )
A. | B. | C. | D. |
B
解析试题分析: .由题意得:
.由题意得: 在
在 上有两个不同的根.
上有两个不同的根.
令 ,则
,则 .
.
所以 是
是 的极小值.
的极小值.
所以
 .
.
考点:1、新定义;2、导数的应用;3、函数的零点.

练习册系列答案
 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
用边长为48厘米的正方形铁皮做一个无盖的铁盒时,在铁皮的四角各截去一个面积相等的小正方形,然后把四边折起,就能焊成铁盒.当所做的铁盒的容积最大时,在四角截去的正方形的边长为( )
| A.12 | B.10 | C.8 | D.6 |
已知 且关于
且关于 的函数
的函数 在
在 上有极值,则
上有极值,则 与
与 的夹角范围是( )
的夹角范围是( )
A. | B. | C. | D. |
曲线 与直线
与直线 及
及 所围成的封闭图形的面积为( )
所围成的封闭图形的面积为( )
A. | B. | C. | D. |
函数f(x)=ln(x+1)- 的零点所在的大致区间是( )
的零点所在的大致区间是( )
| A.(0,1) | B.(1,2) |
| C.(2,e) | D.(3,4) |
若函数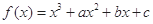 有两个极值点
有两个极值点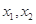 ,且
,且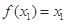 ,则关于
,则关于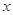 的方程
的方程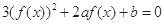 的不同实根个数是( )
的不同实根个数是( )
| A.3 | B.4 | C.5 | D.6 |
若 ,
, ,
, ,则
,则 的大小关系为( )
的大小关系为( )
A. | B. | C. | D. |
已知函数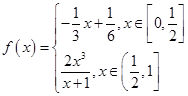 ,函数
,函数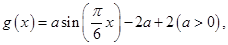 若存在
若存在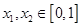 ,使得
,使得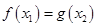 成立,则实数
成立,则实数 的取值范围( )
的取值范围( )
A.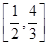 | B.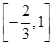 | C.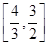 | D.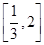 |
 在
在 上可导,其导函数为
上可导,其导函数为 ,若
,若 ,
, ,则下列判断一定正确的是 ( )
,则下列判断一定正确的是 ( )


