题目内容
7.过点(-4,0)的曲线y=$\sqrt{x}$的切线与两坐标所围成三角形的面积为8.分析 求出函数的导数,利用导数的几何意义求出曲线的切线方程,结合三角形的面积公式进行求解即可.
解答 解:函数的导数f′(x)=$\frac{1}{2\sqrt{x}}$,
设切点为(m,$\sqrt{m}$),(m≥0),
则切线斜率k=f′(m)=$\frac{1}{2\sqrt{m}}$,
则对应的切线方程为y-$\sqrt{m}$=$\frac{1}{2\sqrt{m}}$(x-m),
∵切线过点(-4,0),
∴-$\sqrt{m}$=$\frac{1}{2\sqrt{m}}$(-4-m),
即-2m=-4-m,
则m=4,
即切线方程为为y-2=$\frac{1}{4}$(x-4),
即x-4y+8=0,
令x=0,y=2,
令y=0,x=-8,
则切线与坐标轴的交点坐标为(0,2),(-8,0),
则对应的面积S=$\frac{1}{2}×2×8$=8,
故答案为:8.
点评 本小题主要考查导数的概念、导数的几何意义和直线的方程等基本知识.根据导数的几何意义求出切线方程是解决本题的关键.

练习册系列答案
相关题目
17.cos(-1920°)的值为( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
2.在△ABC中.AC=$\sqrt{6}$,BC=2,B=60°,则角C的值为( )
| A. | 45° | B. | 30° | C. | 75° | D. | 90° |
4.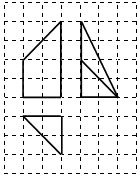 如图网格纸上小正方形的边长为l,粗实线画山的是某几何体的三视图,则这个几何体的体积为( )
如图网格纸上小正方形的边长为l,粗实线画山的是某几何体的三视图,则这个几何体的体积为( )
 如图网格纸上小正方形的边长为l,粗实线画山的是某几何体的三视图,则这个几何体的体积为( )
如图网格纸上小正方形的边长为l,粗实线画山的是某几何体的三视图,则这个几何体的体积为( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |