题目内容

9．函数f（x）的定义域为（-∞，-1）∪（1，+∞），且f（x+1）为奇函数，当x＞1时，f（x）=2x2-12x+16，则函数y=f（x）-2的所有零点之和是5．

分析 f（x+1）为奇函数可得函数f（x）的图象关于（1，0）对称，从而可求x＜1时的函数解析式，进而解方程f（x）=2可得．

解答 解：∵f（x+1）为奇函数，
∴函数图象关于（0，0）对称，
即函数f（x）的图象关于（1，0）对称
∵当x＞1时，f（x）=2x2-12x+16，
当x＜1时，f（x）=-2x2-4x
令2x2-12x+16=2，
即x2-6x+7=0，
可得x1+x2=6，
令-2x2-4x=2，
即x2+2x+1=0，可得x3=-1
∴横坐标之和为x1+x2+x3=6-1=5
故答案为：5．

点评 本题主要考查了函数的平移、奇函数的对称性，利用对称性求函数在对称区间上的解析式．考查性质的灵活应用．

练习册系列答案
相关题目
19．函数y=|logax|，其中0＜a＜1，比较f（2），f（$\frac{1}{4}$），f（$\frac{1}{3}$）的大小．
20．设函数f（x）=x2-1，对任意x∈[3，+∞），f（$\frac{x}{m}$）-4m2f（x）≤f（x-1）+4f（m）恒成立，则实数m的取值范围是$（-∞，-\frac{\sqrt{2}}{2}]∪[\frac{\sqrt{2}}{2}，+∞）$．
17．设a∈R，函数f（x）=cosx（2asinx-cosx）+sin2x的图象的一条对称轴是直线$x=-\frac{π}{6}$．
（Ⅰ）求$f（-\frac{π}{3}）$的值和a的值；
（Ⅱ）求函数f（x）在$[\frac{π}{4}，\frac{π}{2}]$上的最大值和最小值．
4．如图，在四棱锥P-ABCD中，底面是边长为2$\sqrt{3}$的菱形，且∠BAD=120°，且PA⊥平面ABCD，PA=2$\sqrt{6}$，M，N分别为PB，PD的中点．
（1）证明：MN∥平面ABCD；
（2）若$\overrightarrow{PQ}$=$\frac{2}{3}$$\overrightarrow{PC}$，求直线AQ与平面AMN所成角的正弦值．
14．等差数列{an}的公差d≠0，a1=20，且a3，a7，a9成等比数列．Sn为{an}的前n项和，则S10的值为110．
1．在△ABC中，内角A，B，C所对的边分别是a，b，c，若$bsinA=2csinB，a=4，cosB=\frac{1}{4}$，则边长b的等于4．
18．在直角坐标系xOy中，点P（1，0），以原点O为极点，以x轴正半轴为极轴，建立极坐标系，曲线C的方程为：ρ=$\frac{2}{\sqrt{1+3si{n}^{2}θ}}$．
（1）求曲线C的直角坐标方程；
（2）直线L过点P交曲线C于A，B两点，且满足|PA|•|PB|=$\frac{6}{5}$，求直线L的方程．
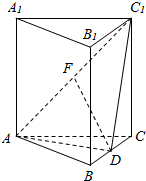19．如图，在直三棱柱ABC-A1B1C1中，AB=AC，BD=DC，AF=C1F．
（1）求证：平面ADC1⊥平面BCC1B1；
（2）求证：DF∥平面A1ABB1．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网