题目内容
18.在直角坐标系xOy中,点P(1,0),以原点O为极点,以x轴正半轴为极轴,建立极坐标系,曲线C的方程为:ρ=$\frac{2}{\sqrt{1+3si{n}^{2}θ}}$.(1)求曲线C的直角坐标方程;
(2)直线L过点P交曲线C于A,B两点,且满足|PA|•|PB|=$\frac{6}{5}$,求直线L的方程.
分析 (1)曲线C的方程为:ρ=$\frac{2}{\sqrt{1+3si{n}^{2}θ}}$,即ρ2+3(ρsinθ)2=4,进而可得曲线C的直角坐标方程;
(2)先设直线方程为是$\left\{\begin{array}{l}x=1+t•cosθ\\ y=sinθ\end{array}\right.$,θ为参数,然后代入椭圆方程得出t1•t2=-$\frac{3}{3si{n}^{2}θ+1}$<0,再根据|PA|•|PB|=-t1•t2,求出θ的值即可求出直线方程.
解答 解:(1)曲线C的方程为:ρ=$\frac{2}{\sqrt{1+3si{n}^{2}θ}}$,即$ρ\sqrt{1+3si{n}^{2}θ}=2$,
即$\sqrt{{ρ}^{2}+3(ρsi{n}^{\;}{θ)}^{2}}=2$,
即ρ2+3(ρsinθ)2=4,
化为直角坐标方程为:x2+y2+3y2=4,
即x2+4y2=4,
即$\frac{{x}^{2}}{4}+{y}^{2}=1$;
(2)设直线l的方程是$\left\{\begin{array}{l}x=1+t•cosθ\\ y=sinθ\end{array}\right.$,θ为参数,代入$\frac{{x}^{2}}{4}+{y}^{2}=1$得:(3sin2θ+1)•t2+2t•cosθ-3=0
∵t1•t2=-$\frac{3}{3si{n}^{2}θ+1}$<0
∴|PA|•|PB|=-t1•t2⇒$\frac{3}{3si{n}^{2}θ+1}$=$\frac{6}{5}$⇒sin2θ=$\frac{1}{2}$,
∴θ=$\frac{π}{4}$或$\frac{3π}{4}$,
所求的直线l的方程是 x+y+1=0或x-y-1=0.
点评 本题考查了椭圆的简单性质,设直线l的方程是$\left\{\begin{array}{l}x=1+t•cosθ\\ y=sinθ\end{array}\right.$,θ为参数,可以是问题简单化,属于中档题

| A. | (-∞,0] | B. | [2,+∞) | C. | (-∞,0]∪[2,+∞) | D. | [0,2] |
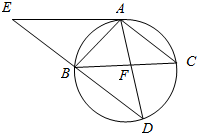 如图,△ABC为圆的内接三角形,BD为圆的弦,且BD∥AC.过点A作圆的切线与DB的延长线交于点E,AD与BC交于点F.若AB=AC,AE=6,BD=5.
如图,△ABC为圆的内接三角形,BD为圆的弦,且BD∥AC.过点A作圆的切线与DB的延长线交于点E,AD与BC交于点F.若AB=AC,AE=6,BD=5.