题目内容
1.在△ABC中,内角A,B,C所对的边分别是a,b,c,若$bsinA=2csinB,a=4,cosB=\frac{1}{4}$,则边长b的等于4.分析 由已知条件利用正弦定理得ba=2cb,从而得到c=2,由此利用余弦定理能求出边长b的值.
解答 解:在△ABC中,内角A,B,C所对的边分别是a,b,c,
∵$bsinA=2csinB,a=4,cosB=\frac{1}{4}$,
∴ba=2cb,从而a=2c,又a=4,所以c=2,
∴$b=\sqrt{{a^2}+{c^2}-2accosB}=\sqrt{{4^2}+{2^2}-2×4×2×\frac{1}{4}}=4$.
故答案为:4.
点评 本题考查三角形的边长的求法,是中档题,解题时要认真审题,注意正弦定理和余弦定理的合理运用.

练习册系列答案
相关题目
16.设不等式组$\left\{\begin{array}{l}{x≥1}\\{x+y≤3}\\{y≥a(x-3)}\end{array}\right.$,其中a>0,若z=2x+y的最小值为$\frac{1}{2}$,则a=( )
| A. | -$\frac{4}{3}$ | B. | $\frac{4}{3}$ | C. | -$\frac{3}{4}$ | D. | $\frac{3}{4}$ |
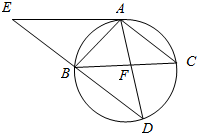 如图,△ABC为圆的内接三角形,BD为圆的弦,且BD∥AC.过点A作圆的切线与DB的延长线交于点E,AD与BC交于点F.若AB=AC,AE=6,BD=5.
如图,△ABC为圆的内接三角形,BD为圆的弦,且BD∥AC.过点A作圆的切线与DB的延长线交于点E,AD与BC交于点F.若AB=AC,AE=6,BD=5.