题目内容
19．
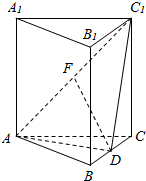如图，在直三棱柱ABC-A1B1C1中，AB=AC，BD=DC，AF=C1F．（1）求证：平面ADC1⊥平面BCC1B1；
（2）求证：DF∥平面A1ABB1．
分析 （1）由等腰三角形底边中线的性质可得AD⊥BC，再由直三棱柱ABC-A1B1C1的性质得到AD⊥CC1，然后利用线面垂直的判断得到AD⊥平面BCC1B1，再由面面垂直的判断得答案；
（2）连结CA1，∵AF=C1F，可得A1F=CF，且A1，F，C共线，进一步得到DF∥BA1，再由线面平行的判定得答案．
解答 
证明：（1）由AB=AC，BD=DC，可得AD⊥BC，
又直三棱柱ABC-A1B1C1中，CC1⊥底面ABC，∴AD⊥CC1，
∵CC1∩BC=C，∴AD⊥平面BCC1B1，
而AD?平面ADC1，
∴平面平面ADC1⊥平面BCC1B1；
（2）连结CA1，∵AF=C1F，
∴F∈CA1，且A1F=CF，
连接BA1，又BD=DC，
∴DF∥BA1，
∵DF?平面A1ABB1，BA1?平面A1ABB1．
∴有DF∥平面A1ABB1．
点评 本题考查平面与平面垂直的判断，考查了直线与平面平行的判断，考查学生的空间想象能力和思维能力，关键是熟记有关定理的内容，是中档题．
练习册系列答案
相关题目
如图，在四棱柱ABCD-A1B1C1D1中，AB∥C1D1，AB1⊥BC，且AA1=AB．