题目内容
3.我们将一个四面体四个角中直角三角形的个数定义为此四面体的直度,在四面体ABCD中,AD⊥平面ABC,AC⊥BC,则四面体ABCD的直度为4.分析 由AD⊥平面ABC,知AD⊥AB,AD⊥AC,从而AD⊥BC,由AC⊥BC,AC∩AD=A,知BC⊥CD,从而四面体ABCD的四个面均为直角三角形.
解答 解:∵在四面体ABCD中,AD⊥平面ABC,
∴AD⊥AB,AD⊥AC,∴AD⊥BC,
∵AC⊥BC,AC∩AD=A,
∴BC⊥平面ACD,∴BC⊥CD,
∴四面体ABCD的四个面均为直角三角形,
∴四面体ABCD的直度为4.
故答案为:4.
点评 本题考查四面体的直度的求法,是基础题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
13.设Sn是等差数列{an}的前项和,若S4≠0,且S8=3S4,设S12=λS8,则λ=( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | 3 |
14.已知扇形的半径为3,圆心角为$\frac{2π}{3}$,则扇形的弧长为( )
| A. | 3π | B. | 2π | C. | 360 | D. | 540 |
11.某几何体的三视图如图所示,则该几何体的体积为( )
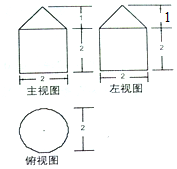

| A. | 2π | B. | $\frac{7}{3}$π | C. | $\frac{8}{3}$π | D. | 4π |
8.已知a=5${\;}^{lo{g}_{2}3.4}$,b=5log43.6,c=($\frac{1}{5}$)${\;}^{lo{g}_{2}0.3}$之间的大小关系为( )
| A. | a>b>c | B. | b>a>c | C. | a>c>b | D. | c>a>b |
9.市教育局为了对学校教学水平和学校管理水平评价,从某校学生中选出200人进行统计,其中对学校教学水平给出好评的学生人数为总数的60%,对学校管理水平给出好评的学生人数为总数的75%,其中对学校教学水平和学校管理水平给出好评的有80人.
(1)填写学校教学水平和学校管理水平评价的2×2列联表:
(2)问:是否可以在犯错误概率不超过0.1%的前提下,认为学校的教学水平好评与学校管理水平好评有关?
$({{k^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}})$其中n=a+b+c+d.
| 对学校管理水平好评 | 对学校管理水平不满意 | 合计 | |
| 对学校教学水平好评 | |||
| 对学校教学水平不满意 | |||
| 合计 |
(2)问:是否可以在犯错误概率不超过0.1%的前提下,认为学校的教学水平好评与学校管理水平好评有关?
| p(k2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |