题目内容
在几何体ABCDE中,∠BAC= ,DC⊥平面ABC,EB⊥平面ABC, AB=AC=BE=2,CD=1.
,DC⊥平面ABC,EB⊥平面ABC, AB=AC=BE=2,CD=1.
(1)设平面ABE与平面ACD的交线为直线 ,求证:
,求证: ∥平面BCDE;
∥平面BCDE;
(2)设F是BC的中点,求证:平面AFD⊥平面AFE;
(3)求几何体ABCDE的体积.
(1)详见解析;(2)详见解析;(3)2.
解析试题分析:(1)根据两条直线同垂直于一个平面,这两条直线平行可得DC//EB,再有直线与平面平行的判定定理得出直线DC∥平面ABE,由于 是平面ABE与平面ACD的交线,可得DC∥
是平面ABE与平面ACD的交线,可得DC∥ ,又由直线与平面平行的判定定理
,又由直线与平面平行的判定定理 ∥平面BCDE.(2)先证AF⊥平面BCDE,再证FD⊥平面AFE,最后证明平面AFD⊥平面AFE.(3)由等体积公式求解,即
∥平面BCDE.(2)先证AF⊥平面BCDE,再证FD⊥平面AFE,最后证明平面AFD⊥平面AFE.(3)由等体积公式求解,即 .
.
【证】(1)∵DC⊥平面ABC,EB⊥平面ABC,
∴DC//EB,又∵DC 平面ABE,EB
平面ABE,EB 平面ABE,
平面ABE,
∴DC∥平面ABE, 平面ABE
平面ABE 平面ACD,则DC∥
平面ACD,则DC∥ ,
,
又
 平面BCDE,CD
平面BCDE,CD 平面BCDE,
平面BCDE,
所以 ∥平面BCDE.(4分)
∥平面BCDE.(4分)
【解】(2)在△DEF中, ,由勾股定理知,
,由勾股定理知,
由DC⊥平面ABC,AF 平面ABC,∴DC⊥AF,
平面ABC,∴DC⊥AF,
又∵AB=AC,F是BC的中点,∴AF⊥BC,
又∵DC∩BC=C,DC 平面BCDE ,BC
平面BCDE ,BC 平面BCDE,
平面BCDE,
∴AF⊥平面BCDE,∴AF⊥FD,又∵AF∩FE=F,∴FD⊥平面AFE,
又FD 平面AFD,故平面AFD⊥平面AFE.(9分)
平面AFD,故平面AFD⊥平面AFE.(9分)
(3) =
= =2.(13分)
=2.(13分)
考点:空间中的线线、线面、面面平行于垂直,三棱锥的体积.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
 中,
中, ,
, ,
,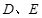 分别为
分别为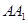 和
和 的中点.
的中点.

 平面
平面 ;(5分)
;(5分) 的体积.(7分)
的体积.(7分) 中,已知平面
中,已知平面 平面
平面 且
且 ,
, .
.
 为棱
为棱 上的一点,且
上的一点,且 平面
平面 ,求线段
,求线段 的长度
的长度
 和
和 都为矩形。
都为矩形。
 ,证明:直线
,证明:直线 平面
平面 ,
, 分别是线段
分别是线段 ,
, 的中点,在线段
的中点,在线段 上是否存在一点
上是否存在一点 ,使直线
,使直线 平面
平面 ?请证明你的结论。
?请证明你的结论。 ,AA′=1,点M,N分别为A′B和B′C′的中点.
,AA′=1,点M,N分别为A′B和B′C′的中点.
 Sh,其中S为底面面积,h为高)
Sh,其中S为底面面积,h为高) 和
和 所在平面互相垂直,且
所在平面互相垂直,且 ,
, ,E、F、G分别为AC、DC、AD的中点.
,E、F、G分别为AC、DC、AD的中点. 平面BCG;
平面BCG; ,其中S为底面面积,h为高.
,其中S为底面面积,h为高.

 ,点H、G分别是线段EF、BC的中点.
,点H、G分别是线段EF、BC的中点. 平面
平面 ;(2)点M在直线EF上,且
;(2)点M在直线EF上,且 平面
平面 ,求平面ACH与平面ACM所成锐角的余弦值.
,求平面ACH与平面ACM所成锐角的余弦值.
