题目内容
如图, 和
和 所在平面互相垂直,且
所在平面互相垂直,且 ,
, ,E、F、G分别为AC、DC、AD的中点.
,E、F、G分别为AC、DC、AD的中点.
(1)求证: 平面BCG;
平面BCG;
(2)求三棱锥D-BCG的体积.
附:椎体的体积公式 ,其中S为底面面积,h为高.
,其中S为底面面积,h为高.
(1)详见解析;(2)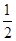
解析试题分析:(1)由已知得, 是
是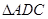 的中位线,故
的中位线,故 ,则可转化为证明
,则可转化为证明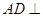 平面BCG.易证
平面BCG.易证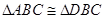 ,则有
,则有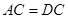 ,则在等腰三角形
,则在等腰三角形 和等腰三角形
和等腰三角形 中,且
中,且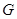 是
是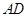 中点,故
中点,故 ,
,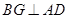 .从而
.从而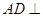 平面BCG,进而
平面BCG,进而 平面BCG;(2)求四面体体积,为了便于计算底面积和高,往往可采取等体积转化法.由平面
平面BCG;(2)求四面体体积,为了便于计算底面积和高,往往可采取等体积转化法.由平面 平面
平面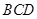 ,利用面面垂直的性质,易作出面
,利用面面垂直的性质,易作出面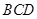 的垂线,同时求出点
的垂线,同时求出点 到面
到面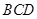 的距离,从而可求出点
的距离,从而可求出点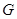 到平面
到平面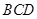 距离,即四面体
距离,即四面体 的高,进而求四面体体积.
的高,进而求四面体体积.
(1)证明:由已知得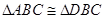 .因此
.因此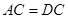 .又
.又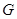 为
为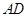 中点,所以
中点,所以 ;同理
;同理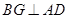 ;因此
;因此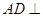 平面
平面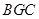 .又
.又 .所以
.所以 平面BCG.
平面BCG.
(2)在平面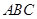 内.作
内.作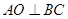 .交
.交 延长线于
延长线于 .由平面
.由平面 平面
平面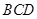 .知
.知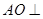 平面
平面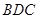 .
.
又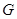 为
为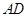 中点,因此
中点,因此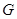 到平面
到平面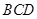 距离
距离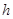 是
是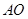 长度的一半.在
长度的一半.在 中,
中, .
.
所以 .
.
考点:1、直线和平面垂直的判定;2、面面垂直的性质;3、四面体的体积.

练习册系列答案
相关题目
 为斜三棱柱
为斜三棱柱 的侧棱
的侧棱 上一点,
上一点,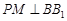 交
交 于点
于点 ,
, 交
交 于点
于点 .
.
 ;
; 中有余弦定理:
中有余弦定理: .
. 中,点
中,点 分别是棱
分别是棱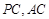 的中点.
的中点.  //平面
//平面 ;
; 平面
平面 ,
, ,求证:
,求证: .
.

 ,DC⊥平面ABC,EB⊥平面ABC, AB=AC=BE=2,CD=1.
,DC⊥平面ABC,EB⊥平面ABC, AB=AC=BE=2,CD=1. ,求证:
,求证:
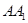 ,
, 为圆柱
为圆柱 的母线,
的母线, 是底面圆
是底面圆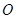 的直径,
的直径,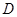 ,
,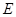 分别是
分别是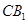 的中点,
的中点,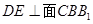 .
. ;
; ;
;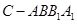 内会有被捕的危险,求鱼被捕的概率.
内会有被捕的危险,求鱼被捕的概率.
 中,底面
中,底面 是正方形,侧棱
是正方形,侧棱 ⊥底面
⊥底面  ,
, 是
是 的中点,作
的中点,作 交
交 于点
于点 .
.
 平面
平面 ;
; 的正弦值.
的正弦值. 
 —
— 中,侧棱垂直底面,
中,侧棱垂直底面, ,
,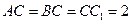 。
。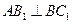 ;
; —
—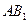 —
—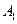 的大小。
的大小。 ,PA=
,PA= ,∠ABC=120°,G为线段PC上的点.
,∠ABC=120°,G为线段PC上的点. 的值.
的值.