题目内容
如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.
(1)求证:AB1⊥面A1BD;
(2)求二面角A-A1D-B的余弦值;
(3)求点C到平面A1BD的距离.
(1)证明过程见解析;(2) ;(3)
;(3)
解析试题分析:(1)取 中点
中点 ,连结
,连结 ,取
,取 中点
中点 ,以
,以 为原点,
为原点, ,
, ,
, 的方向为
的方向为 轴的正方向建立空间直角坐标系,写出
轴的正方向建立空间直角坐标系,写出 坐标,进而得出向量坐标,利用向量垂直时坐标关系可证明
坐标,进而得出向量坐标,利用向量垂直时坐标关系可证明 ,
, ,可得
,可得 平面
平面 ;(2)令平面
;(2)令平面 的法向量为
的法向量为 ,则
,则
 ,可得一法向量
,可得一法向量 ,由(1)
,由(1) 为平面
为平面 的法向量,那么二面角的余弦值即为
的法向量,那么二面角的余弦值即为 ,
, ;(3)可求
;(3)可求 ,
, .
. 为平面
为平面 的法向量,所以C到平面A1BD的距离
的法向量,所以C到平面A1BD的距离 .
.
解:(1)取 中点
中点 ,连结
,连结 .
. 为正三角形,
为正三角形, ,
, 在正三棱柱
在正三棱柱 中,平面
中,平面 平面
平面 ,
, 平面
平面 ,
,
取 中点
中点 ,以
,以 为原点,
为原点, ,
, ,
, 的方向为
的方向为 轴的正方向建立空间直角坐标系,则
轴的正方向建立空间直角坐标系,则 ,
, ,
, ,
, ,
, ,
, ,
, ,
, .
. ,
, ,
, ,
, ,
, 平面
平面 . 4分
. 4分
(2)设平面 的法向量为
的法向量为 ,
, ,
, ,
, ,
, ,
,


令 得
得

练习册系列答案
相关题目
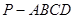 中,底面
中,底面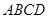 为矩形,
为矩形,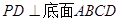 ,
,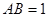 ,
,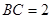 ,
,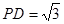 ,
,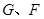 分别为
分别为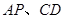 的中点.
的中点.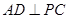 ;
;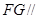 平面
平面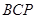 ;
;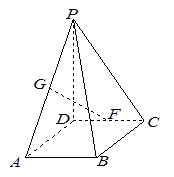
 及其侧视图、俯视图如图所示.设
及其侧视图、俯视图如图所示.设 ,
,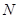 分别为线段
分别为线段 ,
, 的中点,
的中点, 为线段
为线段 上的点,且
上的点,且 .
.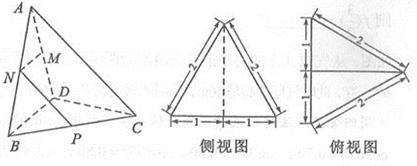
 的余弦值.
的余弦值. ,DC⊥平面ABC,EB⊥平面ABC, AB=AC=BE=2,CD=1.
,DC⊥平面ABC,EB⊥平面ABC, AB=AC=BE=2,CD=1. ,求证:
,求证:
 的底面
的底面 是平行四边形,
是平行四边形, ,
, ,
, 分别是棱
分别是棱 的中点.
的中点. 平面
平面 ;
; ,
,
 中,底面
中,底面 是正方形,侧棱
是正方形,侧棱 ⊥底面
⊥底面  ,
, 是
是 的中点,作
的中点,作 交
交 于点
于点 .
.
 平面
平面 ;
; 的正弦值.
的正弦值. 
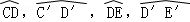 的中点,O1,O1′,O2,O2′分别为CD,C′D′,DE,D′E′的中点.
的中点,O1,O1′,O2,O2′分别为CD,C′D′,DE,D′E′的中点.
 ,ED=1,
,ED=1, //BD,且
//BD,且 .
. 平面BDEF;
平面BDEF;
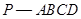 中,
中, ,
, ,
, 为正三角形,且平面
为正三角形,且平面 平面
平面 .
.
 ;
; 的余弦值.
的余弦值.