题目内容
如图,在直三棱柱 中,
中, ,
, ,
,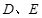 分别为
分别为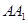 和
和 的中点.
的中点.
(1)求证:
 平面
平面 ;(5分)
;(5分)
(2)求三棱锥 的体积.(7分)
的体积.(7分)
(1)详见解析;(2)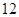 .
.
解析试题分析:(1)这是常规题,只要在平面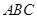 寻找到一条直线与
寻找到一条直线与 平行即可,通常是通过再取中点构造中位线和平行四边形来达到证题目的,这题就是如此;(2)经常是通过体积计算来考查等积变换思想,三棱锥
平行即可,通常是通过再取中点构造中位线和平行四边形来达到证题目的,这题就是如此;(2)经常是通过体积计算来考查等积变换思想,三棱锥 的体积,关键是三棱椎
的体积,关键是三棱椎 的高,直接求有难度,可通过变换顶点达到有利于求高的目的,这里就是转化为求三棱锥
的高,直接求有难度,可通过变换顶点达到有利于求高的目的,这里就是转化为求三棱锥 的体积来实现的.
的体积来实现的.
试题解析:(1)取 边中点
边中点 ,连
,连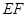 、
、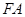 ,则
,则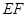

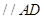 ,且
,且 ,
,
所以四边形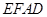 是平行四边形,
是平行四边形,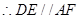 ,且
,且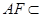 平面
平面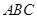 ,
,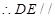 平面
平面 . 5分
. 5分
(2)在等腰三角形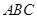 中,易知
中,易知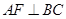 ⊥,又
⊥,又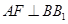 ,∴
,∴ 平面
平面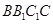
由(1)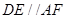 ,
,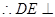 平面
平面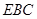
又 ,
, ,
, . 12分
. 12分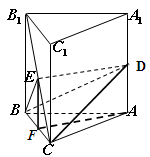
考点:1.立体几何中线面位置关系的证明;2.几何体的体积计算,3.等积变换的思想.

练习册系列答案
相关题目

 底面ABCD,E是PC的中点。
底面ABCD,E是PC的中点。
 为斜三棱柱
为斜三棱柱 的侧棱
的侧棱 上一点,
上一点,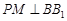 交
交 于点
于点 ,
, 交
交 于点
于点 .
.
 ;
; 中有余弦定理:
中有余弦定理: .
.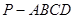 中,底面
中,底面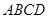 为矩形,
为矩形,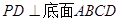 ,
,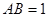 ,
,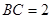 ,
,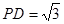 ,
,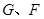 分别为
分别为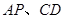 的中点.
的中点.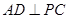 ;
;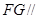 平面
平面 ;
;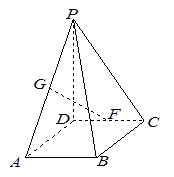
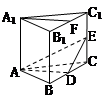
 ,DC⊥平面ABC,EB⊥平面ABC, AB=AC=BE=2,CD=1.
,DC⊥平面ABC,EB⊥平面ABC, AB=AC=BE=2,CD=1. ,求证:
,求证:
 的棱长为3,点
的棱长为3,点 在
在 上,且
上,且 ,点
,点 在平面
在平面 上,且动点
上,且动点 的距离与
的距离与 中,动点
中,动点