题目内容
已知函数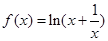 ,且
,且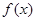 在
在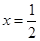 处的切线方程为
处的切线方程为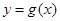 .
.
(1)求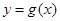 的解析式;
的解析式;
(2)证明:当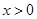 时,恒有
时,恒有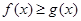 ;
;
(3)证明:若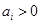 ,
,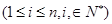 ,且
,且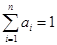 ,则
,则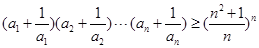 .
.
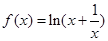 ,且
,且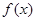 在
在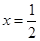 处的切线方程为
处的切线方程为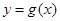 .
.(1)求
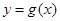 的解析式;
的解析式;(2)证明:当
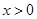 时,恒有
时,恒有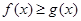 ;
;(3)证明:若
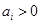 ,
,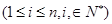 ,且
,且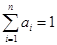 ,则
,则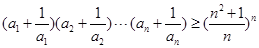 .
.(1) .(2)详见解析.
.(2)详见解析.
 .(2)详见解析.
.(2)详见解析.试题分析:(1)根据导数的几何意义求方程;(2)构造新函数
 用导数法求解;
用导数法求解;试题解析:(1)∵
 ,∴切线斜率
,∴切线斜率 ,
,∴
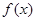 在
在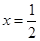 处的切线方程为
处的切线方程为 ,
,即
 . (4分)
. (4分)(2)令
 ,
,∵
 ,
,∴当
 时,
时, ,
, 时,
时, ,∴
,∴ ,
,故
 ,即
,即 . (8分)
. (8分)(3)先求
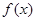 在
在 处的切线方程,由(1)得
处的切线方程,由(1)得 ,
,故
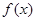 在
在 处的切线方程为
处的切线方程为 ,
,即
 , (10分)
, (10分)下面证明
 ,
,令
 ,
,∵

 ,
,∴
 时,
时, ,
, 时,
时, ,∴
,∴ ,
,∴
 , (12分)
, (12分)∵
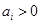 ,∴
,∴ ,
, ,
,∴
 . (14分)
. (14分)
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
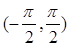 的函数
的函数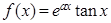
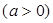 ,在
,在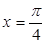 处的切线斜率为
处的切线斜率为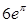
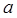 及
及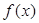 的单调区间;
的单调区间;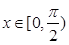 时,
时,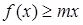 恒成立,求
恒成立,求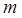 的取值范围.
的取值范围. (
( 为常数),且
为常数),且 在点
在点 处的切线平行于
处的切线平行于 轴.
轴.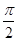 )图像上一个最高点坐标为(2,2
)图像上一个最高点坐标为(2,2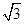 ),这个最高点到相邻最低点的图像与x轴交于点(5,0).
),这个最高点到相邻最低点的图像与x轴交于点(5,0).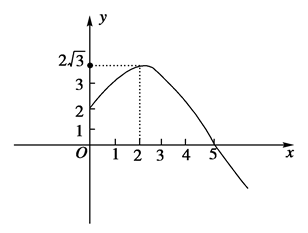
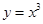 和
和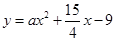 都相切,则
都相切,则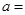 ( )
( )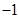 或
或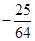
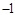 或
或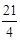
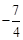 或
或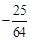
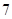
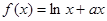 存在与直线
存在与直线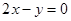 平行的切线,则实数
平行的切线,则实数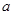 的取值范围是( )
的取值范围是( )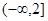
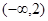
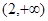
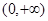

 在点(1,2)处的切线方程为( )
在点(1,2)处的切线方程为( )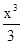 +
+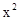 -3x—4在[0,2]上的最小值是
-3x—4在[0,2]上的最小值是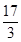
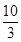
 ,在
,在 时有极值10,则
时有极值10,则 +
+ = _____________
= _____________