题目内容
若存在过点(1,0)的直线与曲线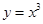 和
和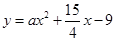 都相切,则
都相切,则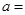 ( )
( )
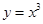 和
和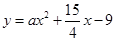 都相切,则
都相切,则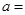 ( )
( )A.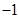 或 或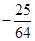 | B.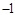 或 或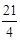 | C.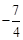 或 或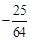 | D.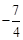 或 或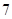 |
A
试题分析:由
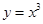 求导得
求导得
设曲线
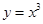 上的任意一点
上的任意一点 处的切线方程为
处的切线方程为 ,将点
,将点 代入方程得
代入方程得 或
或 .
.(1)当
 时:切线为
时:切线为 ,所以
,所以 仅有一解,得
仅有一解,得
(2)当
 时:切线为
时:切线为 ,由
,由 得
得 仅有一解,得
仅有一解,得 .
.综上知
 或
或 .
.
练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
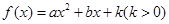 在
在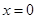 处取得极值,且曲线
处取得极值,且曲线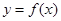 在点
在点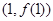 处的切线垂直于直线
处的切线垂直于直线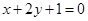 .
.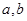 的值;
的值;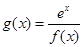 ,讨论
,讨论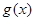 的单调性.
的单调性.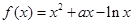 ,
,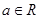 ;
;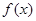 在[1,2]上是减函数,求实数
在[1,2]上是减函数,求实数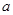 的取值范围;
的取值范围; ,是否存在实数
,是否存在实数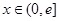 (
(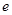 是自然对数的底数)时,函数
是自然对数的底数)时,函数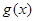 的最小值是
的最小值是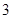 .若存在,求出
.若存在,求出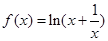 ,且
,且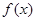 在
在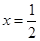 处的切线方程为
处的切线方程为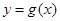 .
.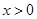 时,恒有
时,恒有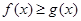 ;
;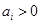 ,
,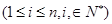 ,且
,且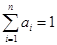 ,则
,则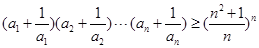 .
.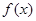 是定义域为
是定义域为 的奇函数,且
的奇函数,且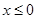 时,
时, ,则函数
,则函数 的导函数在区间
的导函数在区间 上是增函数,则函数
上是增函数,则函数
 在区间
在区间 上是增函数,则实数
上是增函数,则实数 的取值范围为 .
的取值范围为 .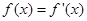 的实数根
的实数根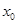 叫做函数
叫做函数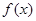 的“新驻点”,若函数
的“新驻点”,若函数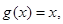
 的“新驻点”分别为
的“新驻点”分别为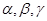 ,则
,则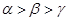
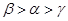
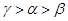
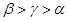
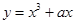 在原点处的切线方程是
在原点处的切线方程是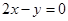 ,则实数
,则实数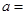 .
.