题目内容
【题目】已知![]() ,
,![]()
(1)求![]() 的单调区间;
的单调区间;
(2)若![]() ,
,![]() 在其公共点
在其公共点![]() 处切线相同,求实数a的值;
处切线相同,求实数a的值;
(3)记![]() ,若函数
,若函数![]() 存在两个零点,求实数a的取值范围.
存在两个零点,求实数a的取值范围.
【答案】(1)函数的单调减区间为:![]() ;增区间为:
;增区间为:![]() (2)
(2)![]() (3)a>e
(3)a>e
【解析】
(1)根据![]() ,求导,由
,求导,由![]() 求减区间,由
求减区间,由![]() 求增区间.
求增区间.
(2)由![]() ,求导
,求导![]() ,根据
,根据![]() ,
,![]() 在其公共点
在其公共点![]() 处切线相同,由
处切线相同,由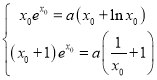 求解.
求解.
(3)易得![]() ,x>0.,求导
,x>0.,求导![]() ,令
,令![]() 得,
得,![]() ,然后分a≤0和a>0两种情况讨论求解.
,然后分a≤0和a>0两种情况讨论求解.
(1)因为![]() ,
,
所以![]() ,
,
得x=-1,
当x<-1时,![]() ;当x>-1时,
;当x>-1时,![]() .
.
所以函数的单调减区间为:![]() ;增区间为:
;增区间为:![]() .
.
(2)由![]() ,
,![]() .
.
因为点![]() 为函数
为函数![]() 的公共点,且函数
的公共点,且函数![]() 在点P处的切线相同,
在点P处的切线相同,
所以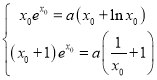 ,且
,且![]() .
.
所以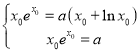 ,
,
即![]() ,
,
显然a≠0,所以![]() .
.
设![]() ,由
,由![]() 得,
得,![]() 在
在![]() 上是单调增函数,
上是单调增函数,
又![]() ,所以
,所以![]() .
.
(3)由![]() 得,
得,![]() ,x>0.
,x>0.
则![]() ,
,
令![]() 得,
得,![]() .
.
设![]() ,由(1)知,
,由(1)知,![]() 在
在![]() 上是单调增函数.
上是单调增函数.
1°当a≤0时,由x>0得,![]() ,
,
所以![]() ,所以
,所以![]() 在
在![]() 上是单调增函数,至多1个零点,不符,舍去.
上是单调增函数,至多1个零点,不符,舍去.
2°当a>0时,因为![]() ,
,![]() ,
,
由零点存在性定理,![]() ,
,![]() 在
在![]() 上是单调增函数且连续,
上是单调增函数且连续,
所以存在唯一![]() ,使得
,使得![]() ,即
,即![]() .
.
当![]() 时,
时,![]() ,
,![]() 单调递减;当
单调递减;当![]() 时,
时,![]() ,
,![]() 单调递增.
单调递增.
因为![]() 存在两个零点,
存在两个零点,
所以![]() ,即
,即![]() ,从而
,从而![]() .
.
所以![]() .
.
因为![]() 在
在![]() 上是单调增函数,
上是单调增函数,
且![]() ,所以
,所以![]() ,
,
由(1)可知,![]() 在
在![]() 是单调递增,
是单调递增,
所以![]() .
.
又![]() ,
,![]() ,
,
而![]() ,易得
,易得![]() ,
,![]() ,
,
所以![]() ,
,
由零点存在性定理知,函数![]() 在
在![]() 上存在唯一一个零点,在
上存在唯一一个零点,在![]() 上存在唯一一个零点,
上存在唯一一个零点,
此时函数![]() 存在两个零点.
存在两个零点.
所以a>e.

【题目】某公司为了对某种商品进行合理定价,需了解该商品的月销售量![]() (单位:万件)与月销售单价
(单位:万件)与月销售单价![]() (单位:元/件)之间的关系,对近
(单位:元/件)之间的关系,对近![]() 个月的月销售量
个月的月销售量![]() 和月销售单价
和月销售单价![]()
![]() 数据进行了统计分析,得到一组检测数据如表所示:
数据进行了统计分析,得到一组检测数据如表所示:
月销售单价 |
|
|
|
|
|
|
月销售量 |
|
|
|
|
|
|
(1)若用线性回归模型拟合![]() 与
与![]() 之间的关系,现有甲、乙、丙三位实习员工求得回归直线方程分别为:
之间的关系,现有甲、乙、丙三位实习员工求得回归直线方程分别为:![]() ,
,![]() 和
和![]() ,其中有且仅有一位实习员工的计算结果是正确的.请结合统计学的相关知识,判断哪位实习员工的计算结果是正确的,并说明理由;
,其中有且仅有一位实习员工的计算结果是正确的.请结合统计学的相关知识,判断哪位实习员工的计算结果是正确的,并说明理由;
(2)若用![]() 模型拟合
模型拟合![]() 与
与![]() 之间的关系,可得回归方程为
之间的关系,可得回归方程为![]() ,经计算该模型和(1)中正确的线性回归模型的相关指数
,经计算该模型和(1)中正确的线性回归模型的相关指数![]() 分别为
分别为![]() 和
和![]() ,请用
,请用![]() 说明哪个回归模型的拟合效果更好;
说明哪个回归模型的拟合效果更好;
(3)已知该商品的月销售额为![]() (单位:万元),利用(2)中的结果回答问题:当月销售单价为何值时,商品的月销售额预报值最大?(精确到
(单位:万元),利用(2)中的结果回答问题:当月销售单价为何值时,商品的月销售额预报值最大?(精确到![]() )
)
参考数据:![]() .
.