题目内容
13．在由数字1，2，3，4，5组成的可重复数字的三位数中，如：213，212，222等表示的数中，只有1个偶数“2”，我们称这样的数只有一个偶数数字，从这样的三位数中任取一个数，则该数是没有重复数字 的三位数的概率为$\frac{18}{37}$．分析 由已知条件先求出偶数数字的个数，再求出从这样的三位数中任取一个数，则该数是没有重复数的三位数的个数，由此能求出该数是没有重复数字的三位数的概率．
解答 解：当偶数数字中只有1个2的个数为：3×3×3=27，
当偶数数字中含有2个2的个数为：3×3=9，
当偶数数字含有3个2的个数为：1，
当偶数数字中只有1个4的个数为：3×3×3=27，
当偶数数字中含有2个4的个数为：3×3=9，
当偶数数字含有3个4的个数为：1，
∴偶数数字的个数为：n=2（27+9+1）=74，
从这样的三位数中任取一个数，则该数是没有重复数 的三位数的个数m=2×（3×3×2）=36，
∴该数是没有重复数字的三位数的概率为：
p=$\frac{m}{n}$=$\frac{36}{74}$=$\frac{18}{37}$．
故答案为：$\frac{18}{37}$．
点评 本题考查概率的求法，是基础题，解题时要认真审题，注意等可能事件的概率计算公式的合理运用．
练习册系列答案
阅读快车系列答案
相关题目
1．已知函数f（x）的定义域为（0，+∞），若y=$\frac{f（x）}{x}$在（0，+∞）上为增函数，则称f（x）为“一阶比增函数”；若y=$\frac{f（x）}{{x}^{2}}$在（0，+∞）上为增函数，则称f（x）为“二阶比增函数”．我们把所有“一阶比增函数”组成的集合记为Ω1，所有“二阶比增函数”组成的集合记为Ω2，．
（Ⅰ）已知函数f（x）=x3-2hx2-hx，若f（x）∈Ω1，且f（x）∉Ω2，求实数h的取值范围；
（Ⅱ）已知0＜a＜b＜c，f（x）∈Ω1且f（x）的部分函数值由下表给出，
求证：d（2d+t-4）＞0；
（Ⅲ）定义集合Ψ={f（x）|f（x）∈Ω2}，且存在常数k，使得任取x∈（0，+∞），f（x）＜k}，请问：是否存在常数m，使得?f（x）∈Ψ，?x∈（0，+∞），有f（x）＜M成立？若存在，求出M的最小值；若不存在，说明理由．
（Ⅰ）已知函数f（x）=x3-2hx2-hx，若f（x）∈Ω1，且f（x）∉Ω2，求实数h的取值范围；
（Ⅱ）已知0＜a＜b＜c，f（x）∈Ω1且f（x）的部分函数值由下表给出，
| x | a | b | c | a+b+c |
| f（x） | d | d | t | 4 |
（Ⅲ）定义集合Ψ={f（x）|f（x）∈Ω2}，且存在常数k，使得任取x∈（0，+∞），f（x）＜k}，请问：是否存在常数m，使得?f（x）∈Ψ，?x∈（0，+∞），有f（x）＜M成立？若存在，求出M的最小值；若不存在，说明理由．
5．已知袋子中装有3个红球、2个白球、1个黑球，如果从中随机任取2个，则下列两个事件中是互斥而不对立的是（ ）
| A． | 至少有一个白球；都是白球 | B． | 至少有一个白球；至少有一个红球 | ||
| C． | 至少有一个白球；红球、黑球各一个 | D． | 恰有一个白球；白球、黑球各一个 |
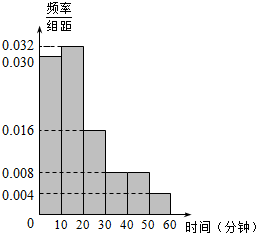某校决定为本校上学时间不少于30分钟的学生提供校车接送服务．为了解学生上学所需时间，从全校600名学生中抽取50人统计上学时间（单位：分钟），现对600人随机编号为001，002，…600．抽取50位学生上学时间均不超过60分钟，将时间按如下方式分成六组，第一组上学时间在[0，10），第二组上学时间在[10，20），…第六组上学时间在[50，60]得到各组人数的频率分布直方图．如图．
已知某个几何体的三视图如图，根据图中标出的尺寸（单位：cm），可得这个几何体的体积是32cm3．