题目内容
18.某学校举办消防知识竞赛,总共7个题中,分值为10分的有A1,A2,A3,A4共4个,分值为20分的有B1,B2,B3 共3个,每位选手都要分别从4个10分题和3个20分题中各随机抽取1题参赛.已知甲选手4个10分题中只有 A2 不会,3个20分题中只会B2.(Ⅰ)求甲选手恰好得30分的概率;
(Ⅱ)求甲选手得分超过10分的概率.
分析 (1)从4个10分题和3个20分题中各抽取1题的基本事件总数n=12,“得30分”这一事件包含的基本事件个数m=3,由此利用等可能事件概率计算公式能求出甲选手恰好得30分的概率.
(Ⅱ)“得分超过10分”这一事件包含的基本事件个数k=4,由此利用等可能事件概率计算公式能求出甲选手得分超过10分的概率.
解答 解:(1)从天而降个10分题和3个20分题中各抽取1题的基本事件空间:
Ω={(A1,B1),(A1,B2),(A1,B3),(A2,B1),(A2,B2),(A2,B3),
(A3,B1),(A3,B2),(A3,B3),(A4,B1),(A4,B2),(A4,B3)},
基本事件总数n=12.(4分)
设“得30分”这一事件为M,则M={(A1,B2),(A3,B2),(A4,B2)},M中包含的基本事件个数m=3.
∴甲选手恰好得30分的概率为P(M)=$\frac{m}{n}=\frac{3}{12}$=$\frac{1}{4}$.(8分)
(Ⅱ)设“得分超过10分”这一事件为N,
则N={(A2,B2),(A1,B2),(A3,B2),(A4,B2)},
N中包含的基本事件个数k=4.
∴甲选手得分超过10分的概率为P(N)=$\frac{k}{n}=\frac{4}{12}=\frac{1}{3}$.(12分)
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.

练习册系列答案
相关题目
9.已知物体的运动方程是s=$\frac{1}{3}$t3-4t2+12t(t表示时间,s表示位移),则瞬时速度为0的时刻是( )
| A. | 0秒、2秒或6秒 | B. | 2秒或16秒 | C. | 2秒、8秒或16秒 | D. | 2秒或6秒 |
6.长为2的线段AB的两个端点分别在x轴和y轴上滑动,那么线段AB中点的轨迹是( )
| A. | 圆 | B. | 椭圆 | C. | 双曲线 | D. | 抛物线 |
3.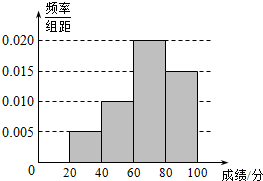 某班学生参加数学测试,成绩的频率分布直方图如图,数据的分组依次为[20,40),[40,60),[60,80),[80,100].若低于60分的人数是18人,则该班的学生人数是( )
某班学生参加数学测试,成绩的频率分布直方图如图,数据的分组依次为[20,40),[40,60),[60,80),[80,100].若低于60分的人数是18人,则该班的学生人数是( )
 某班学生参加数学测试,成绩的频率分布直方图如图,数据的分组依次为[20,40),[40,60),[60,80),[80,100].若低于60分的人数是18人,则该班的学生人数是( )
某班学生参加数学测试,成绩的频率分布直方图如图,数据的分组依次为[20,40),[40,60),[60,80),[80,100].若低于60分的人数是18人,则该班的学生人数是( )| A. | 45 | B. | 50 | C. | 55 | D. | 60 |
10.下列函数是偶函数,且在[0,1]上单调递增的是( )
| A. | y=cos(x+$\frac{π}{2}$) | B. | y=1-2cos22x | C. | y=-x2 | D. | y=|sin(π-x)| |
8.定义在R上的函数f(x)满足f(-x)=-f(x+4),且f(x)在(2,+∞)上为增函数.已知x1+x2<4且(x1-2)•(x2-2)<0,则f(x1)+f(x2)的值( )
| A. | 恒小于0 | B. | 恒大于0 | C. | 可能等于0 | D. | 可正也可负 |