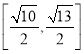题目内容
【题目】动圆![]() 与圆
与圆![]() 外切,并与直线
外切,并与直线![]() 相切,则动圆圆心
相切,则动圆圆心![]() 的轨迹方程为__________,过点
的轨迹方程为__________,过点![]() 作倾斜角互补的两条直线,分别与圆心
作倾斜角互补的两条直线,分别与圆心![]() 的轨迹相交于
的轨迹相交于![]() ,
,![]() 两点,则直线
两点,则直线![]() 的斜率为__________.
的斜率为__________.
【答案】![]()
![]()
【解析】
由已知可得![]() 点到直线
点到直线![]() 的距离等于到点
的距离等于到点![]() 的距离,即动圆圆心
的距离,即动圆圆心![]() 的轨迹是以
的轨迹是以![]() 为焦点,以
为焦点,以![]() 为准线的抛物线,则轨迹方程可求;设出直线
为准线的抛物线,则轨迹方程可求;设出直线![]() 的方程,与抛物线方程联立,求出
的方程,与抛物线方程联立,求出![]() 的坐标,利用斜率公式,即可求得直线
的坐标,利用斜率公式,即可求得直线![]() 的斜率.
的斜率.
解:如图,
由题意可知,![]() ,则
,则![]() ,
,
∴![]() 点到直线
点到直线![]() 的距离等于到点
的距离等于到点![]() 的距离,
的距离,
∴动圆圆心![]() 的轨迹是以
的轨迹是以![]() 为焦点,以
为焦点,以![]() 为准线的抛物线,
为准线的抛物线,
则其轨迹方程为![]() ;
;
点![]() 坐标为
坐标为![]() ,设
,设![]() ,
,
由已知设![]() :
:![]() ,即:
,即:![]() ,
,
代入抛物线的方程得:![]() ,即
,即![]() ,
,
则![]() ,故
,故![]() ,
,
设![]() ,即
,即![]() ,
,
代入抛物线的方程得:![]() ,即
,即![]() ,
,
则:![]() ,故
,故![]() ,
,![]() ,
,
直线AB的斜率![]() ,
,
∴直线AB的斜率为1.
故答案为:![]() ;1.
;1.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目