题目内容
【题目】已知△
的内角
，
，
的对边分别为
，
，
，若
，__________，求△的周长
和面积
.
在①
，
，②
，
，③
，
这三个条件中，任选一个补充在上面问题中的横线处，并加以解答.
【答案】答案不唯一，具体见解析
【解析】
选择①：根据条件求出
，
，则可求出
，再根据正弦定理可求出
，进而可得周长面积；
选择②：
，
，
．由正弦定理可得：
．由余弦定理可得：
，联立解得：
，进而可得周长面积；
选择③：由余弦定理可得
，则周长可求，再根据
可得，通过面积公式可得面积.
解：选①
因为
，
，且
，
，
所以
，
，
在△
中，
，即
，
所以
，
由正弦定理得，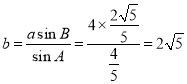
，
因为
，所以
，
所以△的周长
，
△的面积
.
选②
因为，
所以由正弦定理得，
因为，所以
.
又因为.
由余弦定理得
所以
.
解得
.
所以
.
所以△的周长
.
△的面积
.
选③
因为
，
，
所以由余弦定理得，
.
即
.
解得
或
（舍去）.
所以△的周长
，
因为
，
所以
，
所以△的面积
，
故答案为：
选①△的周长
，面积为8；
选②△的周长
，面积为
；
选③△的周长9，面积为
.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
