题目内容
15.已知B、C是两个定点,|BC|=8,且△ABC的周长为18,求这个三角形顶点A的轨迹方程.分析 取BC所在直线为x轴,BC中点为原点,建立如图所示坐标系,由题意可得AB+AC=10>BC,故顶点A的轨迹是以B、C为焦点的椭圆,除去与x轴的交点,利用椭圆的定义和简单性质求出a、b 的值,即得顶点A的轨迹方程.
解答 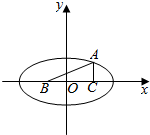 解:取BC所在直线为x轴,BC中点为原点,建立如图所示坐标系,
解:取BC所在直线为x轴,BC中点为原点,建立如图所示坐标系,
∵|BC|=8,且△ABC的周长为18,
∴AB+AC=10>BC,故顶点A的轨迹是以B、C为焦点的椭圆,除去与x轴的交点,
∴2a=10,c=4,
∴a=5,b=3,故顶点A的轨迹方程为$\frac{{x}^{2}}{25}+\frac{{y}^{2}}{9}$=1(y≠0).
点评 本题考查椭圆的定义、标准方程,以及简单性质的应用,注意轨迹方程中y≠0,这是解题的易错点.属于中档题.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
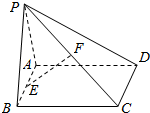 如图,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,AB=1,BC=2,PA=2,E,F分别是AB,PC的中点.
如图,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,AB=1,BC=2,PA=2,E,F分别是AB,PC的中点.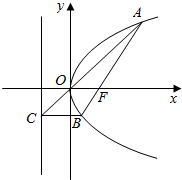 过抛物线y2=2px的焦点F的直线和抛物线相交于A,B两点,如图所示.
过抛物线y2=2px的焦点F的直线和抛物线相交于A,B两点,如图所示.