Question

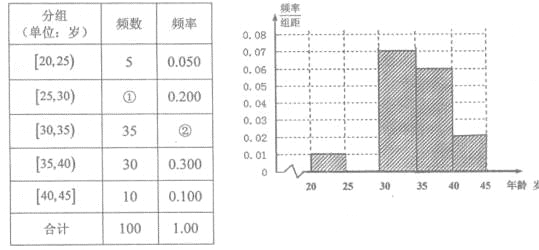
【题目】某校高三年级有1000人，某次考试不同成绩段的人数,且所有得分都是整数.

(1)求全班平均成绩；

(2)计算得分超过141的人数；（精确到整数）

(3)甲同学每次考试进入年级前100名的概率是，若本学期有4次考试， 表示进入前100名的次数，写出的分布列，并求期望与方差.

参考数据： .

Answer 1

【答案】(1) ;(2)23人；（3）见解析.

【解析】试题分析：（1）由易知全班平均成绩；（2）由正太分布曲线的对称性易得 ，从而计算出得分超过141的人数；(3) 的取值为0，1，2，3，4，计算出相应的概率值，利用公式即可算得期望与方差.

试题解析：

(1)由不同成绩段的人数服从正态分布，可知平均成绩.

(2)

,

故141分以上的人数为人.

(3) 的取值为0，1，2，3，4，

,

,

,

,

,

故的分布列为

	0	1	2	3	4

期望，

方差.