题目内容
【题目】已知
是椭圆
的右焦点,过点的直线交椭圆于
两点. 
是
的中点，直线
与直线
交于点
.
（Ⅰ）求征：
；
（Ⅱ）求四边形
面积的最小值.
【答案】（Ⅰ）详见解析；（Ⅱ）
.
【解析】
（Ⅰ）当直线
斜率存在时，设出直线的方程，联立直线方程和抛物线方程后可得中点坐标，故可用直线的斜率表示
的坐标，求出
的斜率后可证
.注意直线斜率不存在的情形.
（Ⅱ）当直线斜率存在时，利用（Ⅰ）的
可以计算
，从而得到
，当直线斜率不存在时，
， 故可得最小值.
（Ⅰ）当直线斜率不存在时，直銭与
轴垂直，
，
,
当直线斜率存在时，设斜率为
，则直线的方程为
，
设
，
，
，则
，
，
联立
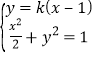得
得，
，
所以直线的方程为
，
，又
，
，
，；
（Ⅱ）当直线斜率不存在时，直线与轴垂直，
，
当直线斜率存在时，
设点
到直线的距离为
，点到直线的距离为
，
则
，
，
，
所以四边形
面积的最小值为
练习册系列答案
相关题目
【题目】某校学生会开展了一次关于“垃圾分类”问卷调查的实践活动，组织部分学生干部在几个大型小区随机抽取了共50名居民进行问卷调查.调查结束后，学生会对问卷结果进行了统计，并将其中一个问题“是否知道垃圾分类方法（知道或不知道）”的调查结果统计如下表：
年龄（岁） |
|
|
|
|
|
|
频数 |
|
| 14 | 12 | 8 | 6 |
知道的人数 | 3 | 4 | 8 | 7 | 3 | 2 |
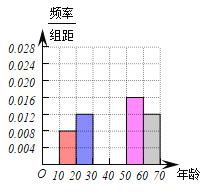
（1）求上表中的
的值，并补全右图所示的的频率直方图；
（2）在被调查的居民中，若从年龄在
的居民中各随机选取1人参加垃圾分类知识讲座，求选中的两人中仅有一人不知道垃圾分类方法的概率.
