题目内容
【题目】![]() 的三个内角
的三个内角![]() ,
,![]() ,
,![]() 所对的边分别为
所对的边分别为![]() ,
,![]() ,
,![]() ,
,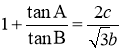 .
.
(1)求![]() 的大小;
的大小;
(2)若![]() 为锐角三角形,求函数
为锐角三角形,求函数![]() 的取值范围;
的取值范围;
(3)现在给出下列三个条件:①![]() ;②
;②![]() ;③
;③![]() ,试从中再选择两个条件以确定
,试从中再选择两个条件以确定![]() ,求出所确定的
,求出所确定的![]() 的面积.
的面积.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)选择①②,
;(3)选择①②,![]() 或选择①③,
或选择①③,![]() .
.
【解析】
试题(1)因为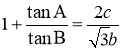 ,切化弦,边化角, 根据
,切化弦,边化角, 根据![]() ,化简整理得
,化简整理得![]() ,
,![]() ; (2)因为
; (2)因为![]() ,所以
,所以![]() ,把
,把![]() 用
用![]() 表示,得关于
表示,得关于![]() 的三角函数
的三角函数![]() ,再根据
,再根据![]() 的范围,求出函数
的范围,求出函数![]() 的取值范围即得函数
的取值范围即得函数![]() 的取值范围;(3)方案一:选择①②,可确定
的取值范围;(3)方案一:选择①②,可确定![]() ,因为
,因为![]() ,
,![]() ,
,![]() ,由余弦定理,得
,由余弦定理,得![]() ,利用
,利用![]() 得
得![]() 的面积.
的面积.
方案二:选择①③,可确定![]() ,因为
,因为![]() ,
,![]() 或
或![]() ,
,![]() ,又
,又![]() ,由正弦定理得边
,由正弦定理得边![]() ,利用
,利用![]() 得
得![]() 的面积.
的面积.
试题解析:(1)因为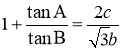 ,由正弦定理,
,由正弦定理,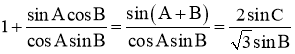
因为![]() ,
,![]() ,所以
,所以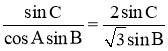
所以![]() ,
,![]()
(2)因为![]() ,
,![]() ,所以
,所以![]()
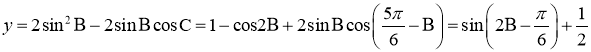 ,
,
又![]() 为锐角三角形,
为锐角三角形,![]()
所以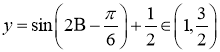
(3)方案一:选择①②,可确定![]() ,因为
,因为![]() ,
,![]() ,
,![]()
由余弦定理,得:
整理得:![]() ,
,![]() ,
,![]()
所以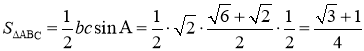
方案二:选择①③,可确定![]() ,
, ![]() ,
,![]()
又![]()
由正弦定理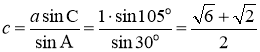
所以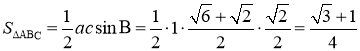
(选择②③不能确定三角形)

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某校高三共有1000位学生,为了分析某次的数学考试成绩,采取随机抽样的方法抽取了50位高三学生的成绩进行统计分析,得到如图所示频数分布表:
分组 |
|
|
|
|
|
频数 | 3 | 11 | 18 | 12 | 6 |
(1)根据频数分布表计算成绩在![]() 的频率并计算这组数据的平均值
的频率并计算这组数据的平均值![]() (同组的数据用该组区间的中点值代替);
(同组的数据用该组区间的中点值代替);
(2)用分层抽样的方法从成绩在![]() 和
和![]() 的学生中共抽取5人,从这5人中任取2人,求成绩在
的学生中共抽取5人,从这5人中任取2人,求成绩在![]() 和
和![]() 中各有1人的概率.
中各有1人的概率.
