题目内容
已知数列{an}满足a1=1,a2=4,an+2+2an=3an+1(n∈N+),设bn=an+1-an.
(1)求数列{bn}、{an}的通项公式;
(2)记{an}的前n项和为Sn,求使得Sn>21-2n成立的最小整数.
(1)求数列{bn}、{an}的通项公式;
(2)记{an}的前n项和为Sn,求使得Sn>21-2n成立的最小整数.
考点:数列递推式,等比关系的确定
专题:点列、递归数列与数学归纳法
分析:(1)利用条件构造数列,先求出数列{bn}的通项公式,然后利用累加法求数列{an}的通项公式;
(2)利用(1)求出{an}的前n项和为Sn,然后解不等式Sn>21-2n求最小整数.
(2)利用(1)求出{an}的前n项和为Sn,然后解不等式Sn>21-2n求最小整数.
解答:
解:(1)由an+2+2an-3an+1=0,得an+2-an+1=2(an+1-an)⇒bn+1=2bn,
∴数列{bn}是以a2-a1=3为首项,公比为2的等比数列,∴bn=3×2n-1(3分)
∴an+1-an=3•2n-1
∴n≥2时,an-an-1=3•2n-2,…,a3-a2=3•2,a2-a1=3,
累加得an-a1=3•2n-2+3•2n-3+…+3•2+3=3(2n-1-1)
∴an=3•2n-1-2(当n=1时,也满足) (6分)
(2)由(1)利用分组求和法得Sn=3(2n-2+2n-3+…+2)-2n=3(2n-1)-2n (9分)
Sn=3(2n-1)-2n>21-2n,得 3•2n>24,即2n>8=23,∴n>3.
∴使得Sn>21-2n成立的最小整数4.(12分)
∴数列{bn}是以a2-a1=3为首项,公比为2的等比数列,∴bn=3×2n-1(3分)
∴an+1-an=3•2n-1
∴n≥2时,an-an-1=3•2n-2,…,a3-a2=3•2,a2-a1=3,
累加得an-a1=3•2n-2+3•2n-3+…+3•2+3=3(2n-1-1)
∴an=3•2n-1-2(当n=1时,也满足) (6分)
(2)由(1)利用分组求和法得Sn=3(2n-2+2n-3+…+2)-2n=3(2n-1)-2n (9分)
Sn=3(2n-1)-2n>21-2n,得 3•2n>24,即2n>8=23,∴n>3.
∴使得Sn>21-2n成立的最小整数4.(12分)
点评:本题主要考查利用数列的递推关系求数列的通项公式,以及利用累加法求数列的通项公式问题,综合性较强.

练习册系列答案
相关题目
与直线x+2y+3=0垂直的抛物线y=x2的切线方程是( )
| A、2x-y-3=0 |
| B、2x-y-1=0 |
| C、2x-y+1=0 |
| D、2x-y+3=0 |
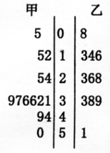 如图为甲、乙两名篮球运动员每场比赛的得分情况的茎叶图,则甲运动员的得分的中位数是
如图为甲、乙两名篮球运动员每场比赛的得分情况的茎叶图,则甲运动员的得分的中位数是