题目内容
3.2016年9月20日在乌鲁木齐隆重开幕的第五届中国-亚欧博览会,其展览规模为历届之最.按照日程安排,22日至25日为公众开放日.某农产品经销商决定在公众开放日开始每天以50元购进农产品若干件,以80元一件销售;若供大于求,剩余农产品当天以40元一件全部退回;若供不应求,则立即从其他地方以60元一件调剂.(1)若农产品经销商一天购进农产品5件,求当天的利润y(单位:元)关于当天需求量n(单位:件,n∈N*)的函数解析式;
(2)农产品经销商记录了30天农产品的日需求量n(单位:件)整理得表:
| 日需求量 | 3 | 4 | 5 | 6 | 7 |
| 频数 | 2 | 3 | 15 | 6 | 4 |
分析 (1)当1≤n≤5时,y=30n+(5-n)×(-10),当n>5时,y=30×5+(n-5)×20.化简整理即可得出.
(2)由已知可得:日需求量为3,频数为2天,利润为70.日需求量为4,频数为3天,利润为110.日需求量为5,频数为15天,利润为150.日需求量为6,频数为6天,利润为170.日需求量为7,频数为4天,利润为190.
∴X的取值为70,110,150,170,190.即可得出分布列与数学期望.
解答 解:(1)当1≤n≤5时,y=30n+(5-n)×(-10)=40n-50.
当n>5时,y=30×5+(n-5)×20=50+20n.
∴函数解析式为y=$\left\{\begin{array}{l}{40n-50,(1≤n≤5)}\\{20n+5,(n>5)}\end{array}\right.$.
(2)由已知可得:日需求量为3,频数为2天,利润为70.
日需求量为4,频数为3天,利润为110.
日需求量为5,频数为15天,利润为150.
日需求量为6,频数为6天,利润为170.
日需求量为7,频数为4天,利润为190.
∴X的取值为70,110,150,170,190.P(X=70)=$\frac{1}{15}$,P(X=110)=$\frac{1}{10}$,P(X=150)=$\frac{1}{2}$,P(X=170)=$\frac{1}{5}$,P(X=190)=$\frac{2}{15}$.
可得X的分布列:
| X | 70 | 110 | 150 | 170 | 190 |
| P | $\frac{1}{15}$ | $\frac{1}{10}$ | $\frac{1}{2}$ | $\frac{1}{5}$ | $\frac{2}{15}$ |
点评 本题考查了分段函数、频率与概率的关系、随机变量的分布列与数学期望,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
18.已知函数f(x)=2sin(ωx+φ)-1(ω>0,|φ|<π)的一个零点是$\frac{π}{3}$,函数y=f(x)图象的一条对称轴是x=-$\frac{π}{6}$,则ω取得最小值时,函数f(x)的单调区间是( )
| A. | [3kπ-$\frac{π}{3}$,3kπ-$\frac{π}{6}$],k∈Z | B. | [3kπ-$\frac{5π}{3}$,3kπ-$\frac{π}{6}$],k∈Z | ||
| C. | [2kπ-$\frac{2π}{3}$,2kπ-$\frac{π}{6}$],k∈Z | D. | [2kπ-$\frac{π}{3}$,2kπ-$\frac{π}{6}$],k∈Z |
8.设函数f(x)=x(lnx-ax)(a∈R)在区间(0,2)上有两个极值点,则a的取值范围是( )
| A. | $(-\frac{1}{2},0)$ | B. | $(0,\frac{ln2+1}{4})$ | C. | $(\frac{1}{2},1)$ | D. | $(\frac{ln2+1}{4},\frac{1}{2})$ |
15.已知命题p:若a,b是实数,则a>b是a2>b2的充分不必要条件;命题q:“?x∈R,x2+2>3x”的否定是“?x∈R,x2+2<3x”,则下列命题为真命题的是( )
| A. | p∧q | B. | ¬p∧q | C. | p∧¬q | D. | ¬p∧¬q |
12.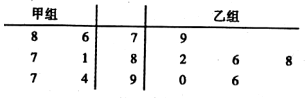 以下茎叶图记录了甲、乙两组各六名学生在一次数学测试中的成绩(单位:分),规定85分以上(含85分)为优秀,现分别从甲、乙两组中随机选取一名同学的数学成绩,则两人成绩都为优秀的概率是( )
以下茎叶图记录了甲、乙两组各六名学生在一次数学测试中的成绩(单位:分),规定85分以上(含85分)为优秀,现分别从甲、乙两组中随机选取一名同学的数学成绩,则两人成绩都为优秀的概率是( )
 以下茎叶图记录了甲、乙两组各六名学生在一次数学测试中的成绩(单位:分),规定85分以上(含85分)为优秀,现分别从甲、乙两组中随机选取一名同学的数学成绩,则两人成绩都为优秀的概率是( )
以下茎叶图记录了甲、乙两组各六名学生在一次数学测试中的成绩(单位:分),规定85分以上(含85分)为优秀,现分别从甲、乙两组中随机选取一名同学的数学成绩,则两人成绩都为优秀的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{4}$ |
13.已知复数z满足(1+i)z=3+i,其中i是虚数单位,则|z|=( )
| A. | 10 | B. | $\sqrt{10}$ | C. | 5 | D. | $\sqrt{5}$ |