题目内容
14.如图,其中有一个是函数f(x)=$\frac{1}{3}$x3+ax2+(a2-1)x+1(a∈R,a≠0)的导函数f′(x)的图象,则f(-1)为( )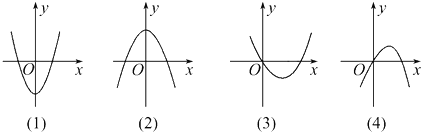
| A. | 2 | B. | -$\frac{1}{3}$ | C. | 3 | D. | -$\frac{1}{2}$ |
分析 求出f(x)的导函数发现为开口向上的抛物线,由a≠0得到其图象必为第(3)个图,由图象知f′(0)=0解得a的值,即可求出f(-1).
解答 解:∵f′(x)=x2+2ax+(a2-1),
∴导函数f′(x)的图象开口向上.
又∵a≠0,∴其图象必为(3).
由图象特征知f′(0)=a2-1=0,且对称轴x=-a>0,
∴a=-1,f(x)=$\frac{1}{3}$x3-x2+1,
故f(-1)=-$\frac{1}{3}$.
故选B.
点评 本题考查导数的运算能力.熟悉函数图象的能力,以及会求函数值的能力,属于中档题.

练习册系列答案
相关题目
9.两个变量y与x的回归模型中,分别选择了4个不同模型,计算出它们的相关指数R2如下,其中拟合效果最好的模型是( )
| A. | 模型1(相关指数2为0.97) | B. | 模型2(相关指数R2为0.89) | ||
| C. | 模型3(相关指数R2为0.56 ) | D. | 模型4(相关指数R2为0.45) |
4.已知二次函数f(x)=x2+bx+c满足f(1)=f(0),则f(-2),f(0),f(2)的大小关系是( )
| A. | f(2)<f(0)<f(-2) | B. | f(0)<f(2)<f(-2) | C. | f(0)<f(-2)<f(2) | D. | 以上都不对 |
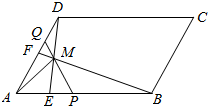 如图所示,在平行四边形ABCD中,$\overrightarrow{AE}$=$\frac{1}{4}$$\overrightarrow{AB}$,$\overrightarrow{AF}$=$\frac{1}{2}$$\overrightarrow{AD}$,BF与DE交于点M,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$.
如图所示,在平行四边形ABCD中,$\overrightarrow{AE}$=$\frac{1}{4}$$\overrightarrow{AB}$,$\overrightarrow{AF}$=$\frac{1}{2}$$\overrightarrow{AD}$,BF与DE交于点M,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$.