Question

3．已知函数f（x）=ln（1+x）-ax的图象在x=1处的切线与直线x+2y-1=0平行．
（1）求函数f（x）的单调递增区间；
（2）若方程f（x）=$\frac{1}{4}$（m-3x）在[2，4]上有两个不相等的实数根，求实数m的取值范围．（参考数据In3≈1.0986
，In4≈1.3863，In5≈1.6094）

Answer 1

分析 （1）求得函数的导数，求得切线的斜率，由直线平行的条件可得a的方程，解方程可得a=1，令导数大于0，求得f（x）的单调区间；
（2）由题意可得m=4ln（1+x）-x在[2，4]上有两个不相等的实数根，由g（x）=4ln（1+x）-x，求得导数，求得单调区间和极值，及端点的函数值，画出图象，即可得到所求m的范围．

解答 解：（1）函数f（x）=ln（1+x）-ax的导数为f′（x）=$\frac{1}{1+x}$-a，
在x=1处的切线斜率为k=$\frac{1}{2}$-a，
由切线与直线x+2y-1=0平行，可得$\frac{1}{2}$-a=-$\frac{1}{2}$，
解得a=1，
则f（x）=ln（1+x）-x的导数为f′（x）=$\frac{1}{1+x}$-1=$\frac{-x}{1+x}$，
当-1＜x＜0时，f′（x）＞0，f（x）递增．
则f（x）的增区间为（-1，0）；
（2）若方程f（x）=$\frac{1}{4}$（m-3x）在[2，4]上有两个不相等的实数根，
即为m=4ln（1+x）-x在[2，4]上有两个不相等的实数根，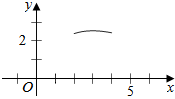
由g（x）=4ln（1+x）-x的导数为g′（x）=$\frac{4}{1+x}$-1=$\frac{3-x}{x+1}$，
当3＜x＜4时，g′（x）＜0，g（x）递减；
当2＜x＜3时，g′（x）＞0，g（x）递增．
g（2）=4ln3-2≈2.3944，g（3）=4ln4-3≈2.5452，
g（4）=4ln5-4≈2.4376．
函数g（x）的图象如右：
作出直线y=m，由图象可得当2.4376≤m＜2.5452时，
方程有两个不相等的实数根．

点评 本题考查导数的运用：求切线的斜率和单调区间，考查函数的零点的求法，运用数形结合的思想方法是解题的关键．