题目内容
5.从混有4件次品的20件商品中抽取3件,已知有1件是次品,求3件都是次品的概率.分析 先求出从混有4件次品的20件商品中抽取3件,基本事件总数,再求出有1件是次品,3件都是次品包含的基本事件个数,由此利用等可能事件概率计算公式能求出有1件是次品,3件都是次品的概率.
解答 解:从混有4件次品的20件商品中抽取3件,已知有1件是次品,
∴抽取的3件产品中至少有一件是次品,基本事件总数n=${C}_{20}^{3}$-${C}_{16}^{3}$,
有1件是次品,3件都是次品包含的基本事件个数m=${C}_{4}^{3}$,
∴有1件是次品,3件都是次品的概率p=$\frac{m}{n}$=$\frac{{C}_{4}^{3}}{{C}_{20}^{3}-{C}_{16}^{3}}$=$\frac{1}{145}$.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.

练习册系列答案
相关题目
15.已知a,b是两条不同的直线.α,β,γ是三个不重合的平面,则下列命题为真命题的是( )
| A. | 若a∥α,α⊥β,则a⊥β | |
| B. | 若a,b与α所成角相等,则a∥b | |
| C. | 若α⊥β,γ⊥β,则α∥γ | |
| D. | 若a,b为异面直线,a?α,a∥β,b?β,b∥α,则α∥β |
16.某工厂统计资料显示,该厂生产的某种产品次品率p与日产量x(千克)(x∈N,且11≤x≤100)的关系如表,
且已知每生产1千克正品盈利a元,每生产1千克次品损失$\frac{a}{2}$元(a>0).
(1)写出生产该产品的日盈利额T(元)表示为日产量x的一个函数关系式;
(2)为了获得最大盈利,该厂生产该产品的日产量应定为多少千克?
| x | 11 | 12 | 13 | 14 | … | 99 | 100 |
| p | $\frac{2}{97}$ | $\frac{1}{48}$ | $\frac{2}{95}$ | $\frac{1}{47}$ | … | $\frac{1}{9}$ | $\frac{1}{4}$ |
(1)写出生产该产品的日盈利额T(元)表示为日产量x的一个函数关系式;
(2)为了获得最大盈利,该厂生产该产品的日产量应定为多少千克?
14.如图,其中有一个是函数f(x)=$\frac{1}{3}$x3+ax2+(a2-1)x+1(a∈R,a≠0)的导函数f′(x)的图象,则f(-1)为( )
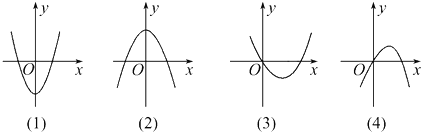
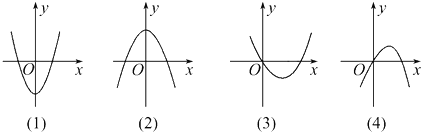
| A. | 2 | B. | -$\frac{1}{3}$ | C. | 3 | D. | -$\frac{1}{2}$ |
 PM2.5是指悬浮在空气中的空气动力学当量直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.根据现行国家标准GB3095-2012,PM2.5日均值在35微克/立方米以下空气质量为一级;在35~75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.
PM2.5是指悬浮在空气中的空气动力学当量直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.根据现行国家标准GB3095-2012,PM2.5日均值在35微克/立方米以下空气质量为一级;在35~75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.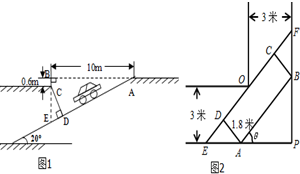 随着私家车的逐渐增多,居民小区“停车难”问题日益突出.本市某居民小区为缓解“停车难”问题,拟建造地下停车库,建筑设计师提供了该地下停车库的入口和进入后的直角转弯处的平面设计示意图.
随着私家车的逐渐增多,居民小区“停车难”问题日益突出.本市某居民小区为缓解“停车难”问题,拟建造地下停车库,建筑设计师提供了该地下停车库的入口和进入后的直角转弯处的平面设计示意图.