题目内容
O为△ABC的外接圆圆心，AB=10，AC=4，∠BAC为钝角，M是边BC的中点，则
•
= ．
| AM |
| AO |
考点：平面向量数量积的运算
专题：计算题,平面向量及应用
分析：结合图形，取AB、AC的中点D、E，地OD⊥AB，OE⊥AC，把求
•
化为求
•
+
•
；再利用数量积的知识求出结果来．
| AM |
| AO |
| AD |
| AO |
| AE |
| AO |
解答：
解：如图所示，取AB、AC的中点D、E，连接OD、OE，
∴OD⊥AB，OE⊥AC；
又∵M是边BC的中点，∴
=
（
+
）；
∴
•
=
（
+
）•
=
•
+
•
=
•
+
•
，
由数量积的定义，
•
=|
|•|
|cos＜
，
＞，
|
|cos＜
，
＞=|
|，
∴
•
=|
|2=（
）2=25，
同理，
•
=|
|2=（
）2=4，
∴
•
=25+4=29．
故答案为：29
解：如图所示，取AB、AC的中点D、E，连接OD、OE，∴OD⊥AB，OE⊥AC；
又∵M是边BC的中点，∴
| AM |
| 1 |
| 2 |
| AB |
| AC |
∴
| AM |
| AO |
| 1 |
| 2 |
| AB |
| AC |
| AO |
| 1 |
| 2 |
| AB |
| AO |
| 1 |
| 2 |
| AC |
| AO |
| AD |
| AO |
| AE |
| AO |
由数量积的定义，
| AD |
| AO |
| AD |
| AO |
| AD |
| AO |
|
| AO |
| AD |
| AO |
| AD |
∴
| AD |
| AO |
| AD |
| 10 |
| 2 |
同理，
| AE |
| AO |
| AE |
| 4 |
| 2 |
∴
| AM |
| AO |
故答案为：29
点评：本题考查了平面向量的数量积的运算性质和三角形外接圆等知识，解题时应结合图形，充分利用平面向量的线性运算与数量积的知识，是中档题．
练习册系列答案
阅读快车系列答案
相关题目
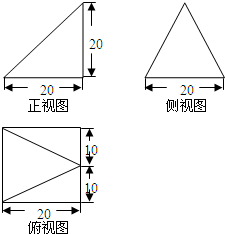已知某个几何体的三视图如图，根据图中标出 的尺寸（单位：cm），则此几何体的所有侧面的面积中最大的是（ ）A、100
| ||
B、100
| ||
C、200
| ||
D、200
|
若x，y满足不等式组
，且y+
x的最大值为2，则实数m的值为（ ）
|
| 1 |
| 2 |
| A、-2 | ||
B、-
| ||
| C、1 | ||
D、
|
过空间两点作直线l的垂面（ ）
| A、能作一个 |
| B、最多只能作一个 |
| C、可作多个 |
| D、以上都不对 |