题目内容
已知函数f(x)＝4sinxcos
＋
.
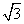(1) 求f(x)的最小正周期；
(2) 求f(x)在区间
上的最大值和最小值及取得最值时x的值．
解：(1) f(x)＝4sinx(cosxcos
－sinxsin)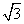＋＝2sinxcosx－2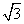sin2x＋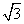
＝sin2x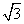＋cos2x＝2sin
.
所以T＝
＝π.
(2) 因为－
≤x≤
，所以－≤2x＋≤
，
所以－
≤sin≤1，所以－1≤f(x)≤2，
当2x＋＝－，即x＝－
时，f(x)min＝－1，
当2x＋＝
，即x＝
时，f(x)max＝2.
练习册系列答案
相关题目
，BC＝2，B＝60°，则边BC上的高为________．
，∠B＝2∠A.
tan10°)．
，则cos2
＝________．
，且270°＜θ＜360°，则sin
＝________，cos
个单位长度，再把所得各点的横坐标伸长到原来的2倍(纵坐标不变)，所得图象的函数解析式是____________________．