题目内容
设{an}是首项为a,公差为d的等差数列(d≠0),Sn是其前n项和.记bn= ,n∈N*,其中c为实数.
,n∈N*,其中c为实数.
(1) 若c=0,且b1,b2,b4成等比数列,证明:Sn k=n2Sk(k,n∈N*);
(2) 若{bn}是等差数列,证明:c=0.
证明:∵ {an}是首项为a,公差为d的等差数列(d≠0),Sn是其前n项和,
∴ Sn=na+ d.
d.
(1) ∵ c=0,∴ bn=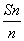 =a+
=a+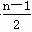 d.
d.
∵ b1,b2,b4成等比数列,∴ b =b1b4,
=b1b4,
∴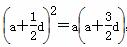
∴  ad-
ad-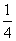 d2=0,
d2=0,
∴ 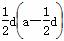 =0.
=0.
∵ d≠0,∴ a= d,∴ d=2a,
d,∴ d=2a,
∴ Sn=na+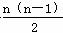 d=na+
d=na+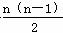 2a=n2a,
2a=n2a,
∴ 左边=Snk=(nk)2a=n2k2a,右边=n2Sk=n2k2a,
∴ 左边=右边,∴ 原式成立.
(2) ∵ {bn}是等差数列,
∴ 设公差为d1,
∴ bn=b1+(n-1)d1
代入bn=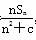 ,得b1+(n-1)d1=
,得b1+(n-1)d1=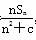 ,
,
∴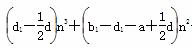 +cd1n=c(d1-b1)对n∈N*恒成立,
+cd1n=c(d1-b1)对n∈N*恒成立,
∴ 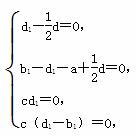
∴ d1= d.∵ d≠0,∴ d1≠0.
d.∵ d≠0,∴ d1≠0.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
 (n∈N*),bn=log2 an,则数列{bn}的前n项和Sn取最大时,n=________.
(n∈N*),bn=log2 an,则数列{bn}的前n项和Sn取最大时,n=________.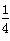 .求:
.求: ,∠B=2∠A.
,∠B=2∠A.