题目内容
20.设z1是已知复数,z为任意复数且|z|=1,2ω=z-z1,则复数ω对应的点的轨迹是( )| A. | 以z1的对应点为圆心,1为半径的圆 | |
| B. | 以-z1的对应点为圆心,1为半径的圆 | |
| C. | 以$\frac{1}{2}$z1的对应点为圆心,$\frac{1}{2}$为半径的圆 | |
| D. | 以-$\frac{1}{2}$z1的对应点为圆心,$\frac{1}{2}$为半径的圆 |
分析 由2ω=z-z1,可得ω+$\frac{1}{2}$z1=$\frac{1}{2}$z,利用|z|=1,即可求出复数ω对应的点的轨迹.
解答 解:∵2ω=z-z1,
∴ω+$\frac{1}{2}$z1=$\frac{1}{2}$z,
∵|z|=1,
∴复数ω对应的点的轨迹是以-$\frac{1}{2}$z1的对应点为圆心,$\frac{1}{2}$为半径的圆,
故选:D.
点评 本题考查复数的几何意义,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
10.若x,y∈R,则“x2>y2”是“x>y”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
11.我们把离心率e=$\frac{\sqrt{5}-1}{2}$的椭圆叫做“优美椭圆”,设椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1为优美椭圆,F、A分别是它的右焦点和左顶点,B是它短轴的一个端点,则∠ABF等于( )
| A. | 60° | B. | 75° | C. | 90° | D. | 120° |
8.过点(2,1)的直线中,被圆(x-1)2+(y-2)2=5截得的最长弦所在的直线方程是( )
| A. | x-y-1=0 | B. | x+y-3=0 | C. | 2x-y-3=0 | D. | x-3y+1=0 |
15.在平面直角坐标系中,若点(2,t)在直线x-2y+4=0的左上方区域且包括边界,则t的取值范围是( )
| A. | t<3 | B. | t>3 | C. | t≥3 | D. | t≤3 |
5.在△ABC中,已知b2+c2-a2+bc=0,则角A等于( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{2π}{3}$ |
12.已知平面α⊥平面β,直线a⊥β,则( )
| A. | a?α | B. | a∥α | C. | a⊥α | D. | a?α或a∥α |
10.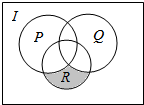 已知全集为I,集合P,Q,R如图所示,则图中阴影部分可以表示为( )
已知全集为I,集合P,Q,R如图所示,则图中阴影部分可以表示为( )
 已知全集为I,集合P,Q,R如图所示,则图中阴影部分可以表示为( )
已知全集为I,集合P,Q,R如图所示,则图中阴影部分可以表示为( )| A. | R∩∁I(P∪Q) | B. | R∩∁I(P∩Q) | C. | (R∩∁IP)∩Q | D. | (R∩∁IQ)∩P |