题目内容
设函数f(x)=x2,则“f(a)>f(b)”是“|a|>|b|”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:根据充分条件和必要条件的定义进行判断即可.
解答:
解:若f(a)>f(b),则a2>b2,即|a|>|b|成立,
若|a|>|b|,则a2>b2,即f(a)>f(b),
故“f(a)>f(b)”是“|a|>|b|”的充要条件,
故选:C
若|a|>|b|,则a2>b2,即f(a)>f(b),
故“f(a)>f(b)”是“|a|>|b|”的充要条件,
故选:C
点评:本题主要考查充分条件和必要条件的判断,比较基础.

练习册系列答案
相关题目
已知
是z的共轭复数,复数z=
,则
•z=( )
| z |
| ||
(1-
|
| z |
A、
| ||
B、
| ||
| C、1 | ||
| D、2 |
执行如图所示的程序框图,输出的S值为( )


| A、162 | B、200 |
| C、242 | D、288 |
根据如图的算法流程图,当输入x的值为3时,输出的结果为( )


| A、5 | B、6 | C、7 | D、8 |
已知圆C:x2+2x+y2=0的一条斜率为1的切线为l1,且与l1垂直的直线l2平分该圆,则直线l2的方程为( )
| A、x-y+1=0 |
| B、x-y-1=0 |
| C、x+y-1=0 |
| D、x+y+1=0 |
下列有关命题的说法错误的是( )
| A、“若a2+b2=0,则a,b全为0”的逆命题是“若a,b不全为0,则a2+b2≠0” |
| B、“x>0”是“x≠0”的必要而不充分条件 |
| C、若p∧q为假命题,且“¬p”为假命题,则q为假命题 |
| D、对于命题p:?x∈R,使得x2+x+1<0,则¬p:?x∈R,均有x2+x+1≥0 |
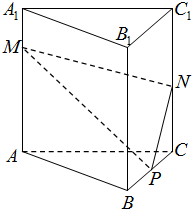 如图,在三棱柱ABC-A1B1C1中,已知侧棱AA1⊥平面ABC,△ABC是边长为2的等边三角形,M是AA1上的一点,AA1=4,A1M=1.P是棱BC上的一点,且由点P沿棱柱侧面经过棱CC1到点M的最短距离为3
如图,在三棱柱ABC-A1B1C1中,已知侧棱AA1⊥平面ABC,△ABC是边长为2的等边三角形,M是AA1上的一点,AA1=4,A1M=1.P是棱BC上的一点,且由点P沿棱柱侧面经过棱CC1到点M的最短距离为3