题目内容
3.设函数f(x)=sinx+sin(x+$\frac{π}{3}$),x∈R.(I)求函数f(x)的单调递增区间;
(Ⅱ)设x1,x2∈[-$\frac{π}{6}$,$\frac{5π}{6}$],若f(x1)=f(x2)(x1≠x2),求f(x1+x2)的值.
分析 (Ⅰ)推导出f(x)=$\sqrt{3}$sin(x+$\frac{π}{3}$),x∈R,由此能求出函数f(x)的单调递增区间.
(Ⅱ)由已知得到f(x1+x2)=$\sqrt{3}sin\frac{5π}{6}=\frac{\sqrt{3}}{2}$,由此能求出f(x1+x2)的值.
解答 解:(Ⅰ)f(x)=sinx+sin(x+$\frac{π}{3}$)
=sinx+sinxcos$\frac{π}{3}$+cosxsin$\frac{π}{3}$
=sinx+$\frac{1}{2}sinx$+$\frac{\sqrt{3}}{2}$cosx
=$\frac{3}{2}sinx+\frac{\sqrt{3}}{2}cosx$
=$\sqrt{3}$sin(x+$\frac{π}{6}$),x∈R.
∴函数f(x)的单调递增区间满足:
$-\frac{π}{2}+2kπ$≤x+$\frac{π}{6}$≤$\frac{π}{2}+2kπ$,k∈Z,
解得-$\frac{2π}{3}$+2kπ≤x≤$\frac{π}{3}+2kπ$,k∈Z,
∴函数f(x)的单调递增区间为[-$\frac{2π}{3}$+2kπ,$\frac{π}{3}+2kπ$],k∈Z.
(Ⅱ)∵f(x)=$\sqrt{3}$sin(x+$\frac{π}{6}$),x1,x2∈[-$\frac{π}{6}$,$\frac{5π}{6}$],
∴${x}_{1}+\frac{π}{6},{x}_{2}+\frac{π}{6}∈[0,π]$,
f(x1)=f(x2)(x1≠x2),
∴$\sqrt{3}sin({x}_{1}+\frac{π}{6})=\sqrt{3}sin({x}_{2}+\frac{π}{6})$,
∴${x}_{1}+\frac{π}{6}+{x}_{2}+\frac{π}{6}=π$,
∴${x}_{1}+{x}_{2}=\frac{2π}{3}$,
f(x1+x2)=$\sqrt{3}sin\frac{5π}{6}=\frac{\sqrt{3}}{2}$.
点评 本题考查三角函数的单调递增区间的求法,考查三角函数值的求法,是中档题,解题时要认真审题,注意三角函数性质的合理运用.

 导学全程练创优训练系列答案
导学全程练创优训练系列答案| A. | 该命题对于n>2的自然数n都成立 | B. | 该命题对于所有的正偶数都成立 | ||
| C. | 该命题何时成立与k取值无关 | D. | 以上答案都不对 |
| A. | 1 | B. | -1 | C. | 4 | D. | -4 |
| A. | -$\frac{11}{3}$ | B. | -$\frac{4}{3}$ | C. | $\frac{4}{3}$ | D. | $\frac{11}{3}$ |
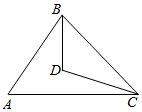 如图,D为△ABC内一点,并且满足AB=CD=4,∠A+∠BDC=180°,试确定S△ABC-S△BDC的最大值.
如图,D为△ABC内一点,并且满足AB=CD=4,∠A+∠BDC=180°,试确定S△ABC-S△BDC的最大值.