题目内容
11.在△ABC中,∠A=$\frac{π}{3}$,AB=2,AC=3,$\overrightarrow{CM}$=2$\overrightarrow{MB}$,则$\overrightarrow{AM}•\overrightarrow{BC}$=( )| A. | -$\frac{11}{3}$ | B. | -$\frac{4}{3}$ | C. | $\frac{4}{3}$ | D. | $\frac{11}{3}$ |
分析 可作出图形,根据$\overrightarrow{CM}=2\overrightarrow{MB}$便可得到$\overrightarrow{AM}=\frac{2}{3}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AC}$,根据条件$∠A=\frac{π}{3}$,AB=2,AC=3进行数量积的运算便可求出$(\frac{2}{3}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AC})•(\overrightarrow{AC}-\overrightarrow{AB})$的值,从而得出$\overrightarrow{AM}•\overrightarrow{BC}$的值.
解答 解:如图,
$\overrightarrow{CM}=2\overrightarrow{MB}$;
∴$\overrightarrow{AM}-\overrightarrow{AC}=2(\overrightarrow{AB}-\overrightarrow{AM})$;
∴$\overrightarrow{AM}=\frac{2}{3}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AC}$;
∴$\overrightarrow{AM}•\overrightarrow{BC}=(\frac{2}{3}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AC})•(\overrightarrow{AC}-\overrightarrow{AB})$
=$\frac{1}{3}\overrightarrow{AB}•\overrightarrow{AC}-\frac{2}{3}{\overrightarrow{AB}}^{2}+\frac{1}{3}{\overrightarrow{AC}}^{2}$
=$\frac{1}{3}×2×3×\frac{1}{2}-\frac{2}{3}×{2}^{2}+\frac{1}{3}×{3}^{2}$
=$\frac{4}{3}$.
故选:C.
点评 考查向量减法的几何意义,向量的数乘运算,以及向量数量积的运算及其计算公式.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | {x|-2<x<2} | B. | {x|-1<x<1} | C. | {x|x≤1} | D. | {x|x>2} |
 与圆
与圆 相交于
相交于 两点,若
两点,若 ,则
,则 的取值范围是______.
的取值范围是______.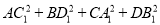 等于( )
等于( )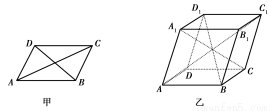
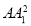 )
)