题目内容
20.函数f(x)=2x-lnx的单调递增区间是$(\frac{1}{2},+∞)$.分析 先求函数的定义域,然后求函数f(x)的导数,令导函数大于0求出x的范围与定义域求交集即可.
解答 x>1解:∵y=x-lnx定义域是{x|x>0}
∵y'=2-$\frac{1}{x}$=$\frac{2x-1}{x}$当 $\frac{2x-1}{x}$>0时,x>$\frac{1}{2}$或x<0(舍)
故答案为:($\frac{1}{2}$,+∞).
点评 本题主要考查函数的单调性与其导函数的正负情况之间的关系.属基础题.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
10.直线y=$\frac{1}{2}$x+b是曲线y=ln x(x>0)的一条切线,则 实数b的值为( )
| A. | 2 | B. | ln 2+1 | C. | ln 2-1 | D. | ln 2 |
11.已知数列{an}中,a1=1,an+1=2an+1(n∈N*),则a4的值为( )
| A. | 31 | B. | 30 | C. | 15 | D. | 63 |
15.已知实数x,y满足不等式组$\left\{\begin{array}{l}y≥x\\ y≤2x\\ x+y≤1\end{array}\right.$,则目标函数z=x+4y的最大值是( )
| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
12.已知函数f(x)=(ex-e-x)x.若f(log3x)+f(log${\;}_{\frac{1}{3}}$x)≤2f(1),则x的取值范围( )
| A. | (-∞$\frac{1}{3}$]∪[3,+∞) | B. | [$\frac{1}{3}$,3] | C. | [$\frac{1}{3}$,1] | D. | [1,3] |
9.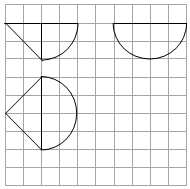 某组合体的三视图如图所示,图中网格每个小正方形的边长为1,曲线均为圆弧的一部分,则该几何体的体积为( )
某组合体的三视图如图所示,图中网格每个小正方形的边长为1,曲线均为圆弧的一部分,则该几何体的体积为( )
 某组合体的三视图如图所示,图中网格每个小正方形的边长为1,曲线均为圆弧的一部分,则该几何体的体积为( )
某组合体的三视图如图所示,图中网格每个小正方形的边长为1,曲线均为圆弧的一部分,则该几何体的体积为( )| A. | $\frac{28}{3}π$ | B. | 4π | C. | $\frac{10}{3}π$ | D. | $\frac{2}{3}+\frac{8}{3}π$ |
10.集合M={x|x=$\frac{k•180°}{2}$±45°,k∈Z},N={x|x=$\frac{k•180°}{4}$±90°,k∈Z},则M、N之间的关系为( )
| A. | M=N | B. | M?N | C. | M?N | D. | M∩N=∅ |
 如图,长方体ABCD-A1B1C1D1中,点M在棱BB1上,两条直线MA,MC与平面ABCD所成角均为θ,AC与BD交于点O.
如图,长方体ABCD-A1B1C1D1中,点M在棱BB1上,两条直线MA,MC与平面ABCD所成角均为θ,AC与BD交于点O.