题目内容
函数y=x2(x>0)的图象在点(ak,ak2)处的切线与x轴交点的横坐标为ak+1( k为正整数),其中a1=16.设正整数数列{bn}满足: ,当n≥2时,有
,当n≥2时,有 .
.
(Ⅰ)求b1,b2,b3,b4的值;
(Ⅱ)求数列{bn}的通项;
(Ⅱ)记 ,证明:对任意n∈N*,
,证明:对任意n∈N*, .
.
 ,当n≥2时,有
,当n≥2时,有 .
.(Ⅰ)求b1,b2,b3,b4的值;
(Ⅱ)求数列{bn}的通项;
(Ⅱ)记
 ,证明:对任意n∈N*,
,证明:对任意n∈N*, .
.解:(Ⅰ)在点(ak,ak2)处的切线方程为:y﹣ak2=2ak(x﹣ak),
当y=0时,解得 ,所以
,所以 ,
,
又∵a1=16,
∴a2=8,a3=4,a4=2

n=2时, ,
,
由已知b1=2,b2=6,得|36﹣2a3|<1,
因为b3为正整数,所以b3=18,同理b4=54
(Ⅱ)由(Ⅰ)可猜想:bn=2·3n﹣1
证明:①n=1,2时,命题成立;
②假设当n=k﹣1与n=k(k≥2且k∈N)时成立,即bk=2·3k﹣1,bk﹣1=2·3k﹣2.
于是 ,整理得:
,整理得:
由归纳假设得:
因为bk+1为正整数,所以bk+1=2·3k
即当n=k+1时命题仍成立.
综上:由知①②知对于 n∈N*,有bn=2·3n﹣1成立
n∈N*,有bn=2·3n﹣1成立
(Ⅲ)证明:由 ③
③
得 ④
④
③式减④式得 ⑤
⑤
 ⑥
⑥
⑤式减⑥式得

=﹣1+2
=1+2
=
=
则 .
.
当y=0时,解得
 ,所以
,所以 ,
,又∵a1=16,
∴a2=8,a3=4,a4=2

n=2时,
 ,
,由已知b1=2,b2=6,得|36﹣2a3|<1,
因为b3为正整数,所以b3=18,同理b4=54
(Ⅱ)由(Ⅰ)可猜想:bn=2·3n﹣1
证明:①n=1,2时,命题成立;
②假设当n=k﹣1与n=k(k≥2且k∈N)时成立,即bk=2·3k﹣1,bk﹣1=2·3k﹣2.
于是
 ,整理得:
,整理得:
由归纳假设得:

因为bk+1为正整数,所以bk+1=2·3k
即当n=k+1时命题仍成立.
综上:由知①②知对于
 n∈N*,有bn=2·3n﹣1成立
n∈N*,有bn=2·3n﹣1成立(Ⅲ)证明:由
 ③
③得
 ④
④③式减④式得
 ⑤
⑤ ⑥
⑥⑤式减⑥式得

=﹣1+2

=1+2

=

=

则
 .
.
练习册系列答案
相关题目
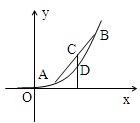 设a,b,λ都为正数,且a≠b,对于函数y=x2(x>0)图象上两点A(a,a2),B(b,b2).
设a,b,λ都为正数,且a≠b,对于函数y=x2(x>0)图象上两点A(a,a2),B(b,b2).