题目内容

曲线y=x2-2x+1在点（1，0）处的切线方程为
 
．
考点：利用导数研究曲线上某点切线方程
专题：计算题,导数的概念及应用
分析：先求导数，因为函数在切点处的导数就是切线的斜率，求出斜率，即可求出曲线y=x2-2x+1在点（1，0）处的切线方程．
解答： 解：曲线y=x2-2x+1的导数为y′=2x-2，
∴曲线y=x2-2x+1在点（1，0）处的切线斜率为0
∴切线方程是y=0．
故答案为：y=0．
点评：本题考查导数的几何意义、利用导数研究曲线上某点切线方程等基础知识．属于基础题．
练习册系列答案
相关题目
在△ABC中，A=60°，B=45°，b=2
2
，则a=
 
．
对酷爱运动的年轻夫妇，让刚满十个月大的婴儿把“0，0，2，8，北，京”六张卡片排成一行，若婴儿能使得排成的顺序为“2008北京”或“北京2008”，则受到父母的夸奖，那么婴儿受到夸奖的概率为
 
．
设函数f（θ）=
sinθ
3
+
3
cosθ
2
+tanθ，则f′（0）=
 
．
在边长为1正三角形ABC中，
AB
•
CA
=
 
．
A、B、C、D、E五人站成一排，如果A必须站在B的左边，则不同排法有（　　）
A、24种B、60种
C、90种D、120种
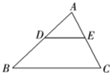如图，已知D、E分别是△ABC的AB、AC边上一点，DE∥BC，且S△ADE：S四边形DBCE=1：3，那么AD：AB等于（　　）
A、1：
3
B、1：2
C、1：3
D、1：4
（1-ax+by）n展开式中不含x的项的系数绝对值的和为243，不含y的项的系数绝对值的和为32，则a，b，n的值可能为（　　）
A、a=2，b=-1，n=5
B、a=-1，b=2，n=6
C、a=-1，b=2，n=5
D、a=-2，b=-1，n=6
若a＜b＜0，则下列不等式中成立的是（　　）
A、
1
a
＜
1
b
B、b+
1
a
＞a+
1
b
C、a+
1
b
＞b+
1
a
D、
b
a
＜
b+1
a+1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网