题目内容
20.函数$y=\frac{2}{π}x-sinx$的部分图象可能是( )| A. |  | B. | 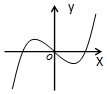 | C. | 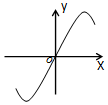 | D. | 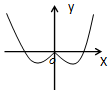 |
分析 利用函数的奇偶性排除选项,利用函数的导数判断函数的单调性以及极值推出结果即可.
解答 解:函数$y=\frac{2}{π}x-sinx$是奇函数,排除D,
并且x=$\frac{π}{2}$时,y=0,
函数$y=\frac{2}{π}x-sinx$的导数为:y′=$\frac{2}{π}$-cosx,导函数有无数个极值点,
存在x0∈(0,$\frac{π}{2}$),使得$\frac{2}{π}$-cosx=0,x∈(0,x0),函数是减函数,
x∈(x0,$\frac{π}{2}$)函数是增函数,
故选:B.
点评 本题考查函数的导数的应用,函数的图象的判断,考查计算能力.

练习册系列答案
相关题目
10.在区间[0,$\frac{π}{2}$]上随机地取一个数x,则事件“$\frac{1}{2}$≤sin x≤$\frac{{\sqrt{3}}}{2}$”发生的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
15.复数z满足(z+2)i=3-2i,则z的共轭复数为( )
| A. | 4+3i | B. | 4-3i | C. | -4+3i | D. | -4-3i |
5.已知$A(3,0),B(0,3),C(cosα,sinα),\overrightarrow{AC}⊥\overrightarrow{BC}$,则sin2α的值为( )
| A. | $\frac{8}{9}$ | B. | $-\frac{8}{9}$ | C. | $\frac{{2\sqrt{2}}}{3}$ | D. | $-\frac{{2\sqrt{2}}}{3}$ |
10.已知集合A={x||x+1|≥1},B={x|x≥-1},则(∁RA)∩B=( )
| A. | [-1,0] | B. | [-1,0) | C. | (-2,-1) | D. | (-2,-1] |
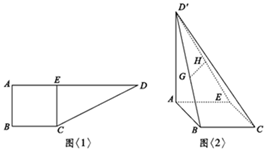 如图<1>:在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=BC=2,AD=6,CE⊥AD于E点,把△DEC沿CE折到D′EC的位置,使D′A=2$\sqrt{3}$,如图<2>:若G,H分别为D′B,D′E的中点.
如图<1>:在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=BC=2,AD=6,CE⊥AD于E点,把△DEC沿CE折到D′EC的位置,使D′A=2$\sqrt{3}$,如图<2>:若G,H分别为D′B,D′E的中点.