��Ŀ����
4����֪ij�߲��̵����������x���֣����������y���죩֮��Ĺ�ϵ�����ʾ��| x | 2 | 3 | 4 | 5 | 6 | 7 | 9 | 12 |
| y | 1 | 2 | 3 | 3 | 4 | 5 | 6 | 8 |
��������ݱ������������������л���ɢ��ͼ��
��������ݱ����ṩ�����ݣ�����С���˷����y����x�����Իع鷽��$\widehaty=\widehatbx+\widehata$������$\widehatb$����2λ��Ч���֣���
�����ݣ����еļ������������߲��̵��������40�֣���Ԥ�ƿ������۶����죨������������������
����$\widehatb=\frac{{\sum_{i=1}^n{{x_i}{y_i}}-n\overline x\overline y}}{{\sum_{i=1}^n{x_i^2}-n{{\overline x}^2}}}$��$\widehata=\overline y-\widehatb\overline x$��
���� �����ݱ������ݻ���ɢ��ͼ���ɣ�
���������⣬����$\overline x$��$\overline y$������ع�ϵ����д���ع�ֱ�߷��̣�
�����ɻع鷽�̼���x=40ʱy��ֵ���ɣ�
��� �⣺�����ݱ������ݻ���ɢ��ͼ������ʾ��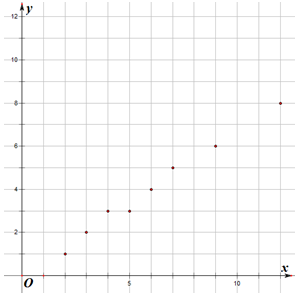
���������⣬����$\overline x$=$\frac{1}{8}$��2+3+4+5+6+7+9+12��=6��
$\overline y$=$\frac{1}{8}$��1+2+3+3+4+5+6+8��=4��
$\sum_{i=1}^8{x{\;}_i^2}=4+9+16+25+36+49+81+144=364$��
$\sum_{i=1}^8{x_i}{y_i}=2+6+12+15+24+35+54+96=244$��
��ع�ϵ��Ϊ$\widehatb=\frac{{\sum_{i=1}^8{x_i}{y_i}-8\overline x\overline y}}{{\sum_{i=1}^8{x{\;}_i^2}-8{{\overline x}^2}}}=\frac{244-8��6��4}{{364-8��{6^2}}}=\frac{52}{76}=0.68$��
��$\widehata=4-0.68��6=-0.08$��
��ع�ֱ�߷���Ϊ$\widehaty=0.68x-0.08$��
�����ɣ���֪��x=40ʱ��y=0.68��40-0.08��27��
���������40�֣�Ԥ�ƿ�����27�죮
���� ���⿼���˻ع�ֱ�߷��̵�����Ӧ�����⣬�ǻ����⣮

��ϰ��ϵ�д�
�����Ŀ
7����֪˫����C1��$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1��a��0��b��0������ΪM��������C2��y2=-2ax�Ľ���ΪF����������C1�Ľ������ϴ��ڵ�Pʹ��PM��PF����˫����C1�����ʵ�ȡֵ��Χ�ǣ�������
| A�� | ��1��2�� | B�� | $��{1��\frac{{3\sqrt{2}}}{4}}]$ | C�� | ��1��+�ޣ� | D�� | $��{\frac{{3\sqrt{2}}}{4}��2}��$ |
15����x��y����Լ������$\left\{\begin{array}{l}x-y+1��0\\ x+y-3��0\\ y��4\end{array}\right.$��z=ax+y����СֵΪ1������ʵ��a��ֵΪ��������
| A�� | 10 | B�� | 8 | C�� | 3 | D�� | 2 |
19����֪����$f��x��=2sin��\frac{��}{4}-2x��$������f��x���ĵ����ݼ�����Ϊ��������
| A�� | $[{\frac{3��}{8}+2k��\frac{7��}{8}+2k��}]��k��Z��$ | B�� | $[{-\frac{��}{8}+2k��\frac{3��}{8}+2k��}]��k��Z��$ | ||
| C�� | $[{\frac{3��}{8}+k��\frac{7��}{8}+k��}]��k��Z��$ | D�� | $[{-\frac{��}{8}+k��\frac{3��}{8}+k��}]��k��Z��$ |
9����֪a=21.3��b=40.7��c=log38����a��b��c�Ĵ�С��ϵΪ��������
| A�� | a��c��b | B�� | b��c��a | C�� | c��a��b | D�� | c��b��a |
16��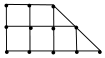 ijũ�������֣�һ����������ջ��� y����λ��kg���������������������� x����������ع�ϵ����ν��������������ָ���ǵ�ֱ�߾��벻���� 1m�������ֱ��¼��������������Ϊ 1��2��3��5��6��7ʱ������������ջ�����������������
ijũ�������֣�һ����������ջ��� y����λ��kg���������������������� x����������ع�ϵ����ν��������������ָ���ǵ�ֱ�߾��벻���� 1m�������ֱ��¼��������������Ϊ 1��2��3��5��6��7ʱ������������ջ�����������������
��1�������������ջ��� y����������������������x�����Իع鷽�̣�
��2��ũ��������ͼ��ʾ��ֱ�����εؿ��ÿ����㣨ָ�ݡ���ֱ�ߵĽ���㣩��������һ������ͼ��
ÿ��С�����εı߳���Ϊ 1������ֱ�����εؿ�ı߽���ڲ������ѡȡһ�������������������
����������������3kg�ĸ��ʣ�
��������һ�����ݣ�x1��y1������x2��y2����������xn��yn������ع�ֱ��y=bx+a��б�ʺͽؾ����С���˹�
�Ʒֱ�Ϊ��$b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2}-n{{��\overline x��}^2}}}=\frac{{\sum_{i=1}^n{��{x_i}-\overline x����{y_i}-\overline y}��}}{{\sum_{i=1}^n{{{��{x_i}-\overline x��}^2}}}}$��$a=\overline y-b\overline x$��
 ijũ�������֣�һ����������ջ��� y����λ��kg���������������������� x����������ع�ϵ����ν��������������ָ���ǵ�ֱ�߾��벻���� 1m�������ֱ��¼��������������Ϊ 1��2��3��5��6��7ʱ������������ջ�����������������
ijũ�������֣�һ����������ջ��� y����λ��kg���������������������� x����������ع�ϵ����ν��������������ָ���ǵ�ֱ�߾��벻���� 1m�������ֱ��¼��������������Ϊ 1��2��3��5��6��7ʱ������������ջ�����������������| x | 1 | 2 | 3 | 5 | 6 | 7 |
| y | 60 | 55 | 53 | 46 | 45 | 41 |
��2��ũ��������ͼ��ʾ��ֱ�����εؿ��ÿ����㣨ָ�ݡ���ֱ�ߵĽ���㣩��������һ������ͼ��
ÿ��С�����εı߳���Ϊ 1������ֱ�����εؿ�ı߽���ڲ������ѡȡһ�������������������
����������������3kg�ĸ��ʣ�
��������һ�����ݣ�x1��y1������x2��y2����������xn��yn������ع�ֱ��y=bx+a��б�ʺͽؾ����С���˹�
�Ʒֱ�Ϊ��$b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2}-n{{��\overline x��}^2}}}=\frac{{\sum_{i=1}^n{��{x_i}-\overline x����{y_i}-\overline y}��}}{{\sum_{i=1}^n{{{��{x_i}-\overline x��}^2}}}}$��$a=\overline y-b\overline x$��