题目内容
在等比数列{an}中,a1=2,且an+1=an+2n.
(1)求数列{an}的通项an;
(2)数列{an}中是否存在这样的两项ap,aq(p<q),使得ap+aq=2 014?若存在,求符合条件的所有的p,q;若不存在,请说明理由.
解:(1)a2=a1+21,
a3=a2+22,
…
an=an-1+2n-1(n≥2).
各式相加,可得
an=a1+21+22+…+2n-1=2+ =2n(n≥2).
=2n(n≥2).
又a1=2=21,
∴an=2n.
(2)假设存在这样的两项ap,aq(p<q)满足条件,则
当q>p≥2时,ap+aq=2p+2q=2p(1+2q-p)是4的倍数,但2 014不是4的倍数.
当p=1时,2 014=ap+aq=21+2q,故2q=2 012.
∵不存在正整数q使2q=2 012,
∴不存在满足条件的p,q.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,则f(3)的值为 ( )
,则f(3)的值为 ( ) B.
B.  C.1 D. 2
C.1 D. 2 =( )
=( )
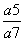 =( )
=( )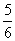 B.
B.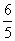 C.
C.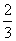 D.
D.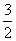
 ,a8·a9=-
,a8·a9=- ,则
,则 +
+ +
+ +
+ =________.
=________.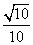 B.
B.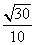 C.
C.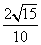 D.
D.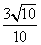
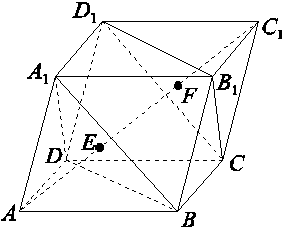
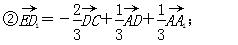 ③设A1D1中点为M,CD的中点为N,则直线MN与平面A1DB有一个交点;
③设A1D1中点为M,CD的中点为N,则直线MN与平面A1DB有一个交点;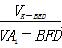 为定值.
为定值.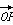 =a
=a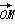 +b
+b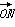 (a,b∈R),其中O为抛物线C的顶点.
(a,b∈R),其中O为抛物线C的顶点.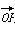 与
与