题目内容
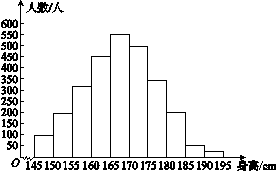
已知三次函数f(x)＝ax3＋bx2＋cx＋d的图象如图所示，则
＝( )
A．5 B．－5 C．2 D．－2
D
[解析] 对f(x)求导，得f′(x)＝3ax2＋2bx＋c，结合题中图象知，x＝－1,2为导函数的零点，所以f′(－1)＝f′(2)＝0，
所以f′(x)＝－
x2＋x＋c＝－(x2－x－2)，
于是
＝－2.故选D.
练习册系列答案
相关题目
，
，则
等于 （ ）
B、
C、
D、
：
，
，那么命题
为 ( )
，
B.
D.某体育用品商场经营一批每件进价为40元的运动服，先做了市场调查，得到数据如下表：
| 销售单价x（元） | 60 | 62 | 64 | 66 | 68 | … |
| 销售量y（件） | 600 | 580 | 560 | 540 | 520 | … |
根据表中数据，解答下列问题：
⑴ 建立一个恰当的函数模型，使它能较好地反映销售量y（件）与销售单价x（元）之间的函数关系，并写出这个函数模型的解析式
；
⑵ 试求销售利润z（元）与销售单价x（元）之间的函数关系式（销售利润 ＝ 总销售收入 － 总进价成本）并求价格为多少利润最大？
上的函数f(x)，f′(x)是它的导函数，且恒有f(x)<f′(x)·tan x成立，则( )
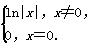以上函数是“H函数”的所有序号为________．
，则S5＝( )
