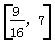题目内容
直线x=1与抛物线C:y2=4x交于M,N两点,点P是抛物线C准线上的一点,记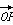 =a
=a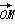 +b
+b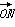 (a,b∈R),其中O为抛物线C的顶点.
(a,b∈R),其中O为抛物线C的顶点.
(1)当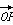 与
与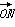 平行时,b=________;
平行时,b=________;
(2)给出下列问题:
①∀a,b∈R,△PMN不是等边三角形;
②∃a<0且b<0,使得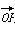 与
与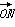 垂直;
垂直;
③无论点P在准线上如何运动,a+b=-1总成立.
其中,所有正确命题的序号是________.
(1)-1 (2)①②③
[解析] (1)当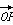 与
与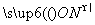 平行时,根据图形的对称知原点O为线段PN的中点,则
平行时,根据图形的对称知原点O为线段PN的中点,则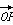 =-
=-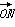 ,所以b=-1.
,所以b=-1.
(2)若△PMN为等边三角形,则P点为准线x=-1与x轴的交点,由题意P(-1,0),可取M(1,2),N(1,-2),|MN|=4,则|PM|=|PN|=2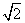 ≠|MN|,故①正确;设P(-1,y),令
≠|MN|,故①正确;设P(-1,y),令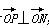 则(-1,y)·(1,-2)=0,即y=-
则(-1,y)·(1,-2)=0,即y=-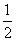 ,则
,则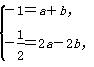 解得a=-
解得a=-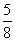 ,b=-
,b=-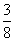 ,故②正确;根据图形的对称性知,点P关于原点的对称点Q必在直线MN上,则
,故②正确;根据图形的对称性知,点P关于原点的对称点Q必在直线MN上,则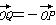 =
=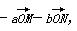 由于点M,N,Q三点共线,则(-a)+(-b)=1,即a+b=-1,故③正确.综上可知,①②③正确.
由于点M,N,Q三点共线,则(-a)+(-b)=1,即a+b=-1,故③正确.综上可知,①②③正确.

 轻松暑假总复习系列答案
轻松暑假总复习系列答案某体育用品商场经营一批每件进价为40元的运动服,先做了市场调查,得到数据如下表:
| 销售单价x(元) | 60 | 62 | 64 | 66 | 68 | … |
| 销售量y(件) | 600 | 580 | 560 | 540 | 520 | … |
根据表中数据,解答下列问题:
⑴ 建立一个恰当的函数模型,使它能较好地反映销售量y(件)与销售单价x(元)之间的函数关系,并写出这个函数模型的解析式 ;
;
⑵ 试求销售利润z(元)与销售单价x(元)之间的函数关系式(销售利润 = 总销售收入 - 总进价成本)并求价格为多少利润最大?
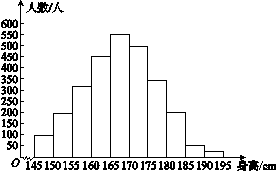
2013年12月21日上午10时,石家庄首次启动重污染天气Ⅱ级应急响应,正式实施机动车尾号限行,当天某报社为了解公众对“车辆限行”的态度,随机抽查了50人,将调查情况进行整理后制成下表:
| 年龄/岁 | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 4 | 6 | 9 | 6 | 3 | 4 |
(1)完成被调查人员的频率分布直方图;
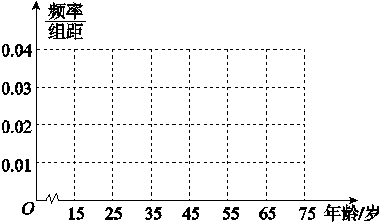
(2)若从年龄在[15,25),[25,35)的调查者中各随机选取两人进行追踪调查,记选中的4人中不赞成“车辆限行”的人数为ξ,求随机变量ξ的分布列和数学期望.
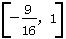
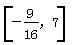 D.
D.