题目内容
14.已知函数f(x)=ln($\sqrt{1+9{x}^{2}}$-3x)+1,若f(a)=$\frac{1}{3}$,则f(-a)的值为( )| A. | -$\frac{1}{3}$ | B. | 2 | C. | $\frac{1}{3}$ | D. | $\frac{5}{3}$ |
分析 利用函数的奇偶性的性质推出ln($\sqrt{1+9{a}^{2}}$-3a)的值,然后求解即可.
解答 解:函数f(x)=ln($\sqrt{1+9{x}^{2}}$-3x)+1,若f(a)=$\frac{1}{3}$,
可得ln($\sqrt{1+9{a}^{2}}$-3a)+1=$\frac{1}{3}$,∴ln($\sqrt{1+9{a}^{2}}$-3a)=$-\frac{2}{3}$.
函数g(x)=ln($\sqrt{1+9{x}^{2}}$-3x)是奇函数,g(-a)=-g(a)
f(-a)=-[ln($\sqrt{1+9{a}^{2}}$-3a)]+1=$\frac{2}{3}+1$=$\frac{5}{3}$.
故选:D.
点评 本题考查函数的奇偶性的应用,函数的零点与方程的跟的关系,考查计算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.函数$f(x)={log_{\frac{1}{2}}}$cosx在x∈(0,2π)时的单调递增区间是( )
| A. | $({0,\frac{π}{2}})$ | B. | (0,π) | C. | (π,2π) | D. | $({\frac{3π}{2},2π})$ |
2.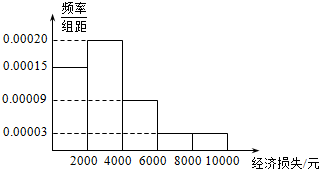 2015年7月9日21时15分,台风“莲花”在我国广东省陆丰市甲东镇沿海登陆,造成165.17万人受灾,5.6万人紧急转移安置,288间房屋倒塌,46.5千公顷农田受灾,直接经济损失12.99亿元.距离陆丰市222千米的梅州也受到了台风的影响,适逢暑假,小明调查了梅州某小区的50户居民由于台风造成的经济损失,将收集的数据分成[0,2000],(2000,4000],(4000,6000],(6000,8000],(8000,10000]五组,并作出如下频率分布直方图(图1):
2015年7月9日21时15分,台风“莲花”在我国广东省陆丰市甲东镇沿海登陆,造成165.17万人受灾,5.6万人紧急转移安置,288间房屋倒塌,46.5千公顷农田受灾,直接经济损失12.99亿元.距离陆丰市222千米的梅州也受到了台风的影响,适逢暑假,小明调查了梅州某小区的50户居民由于台风造成的经济损失,将收集的数据分成[0,2000],(2000,4000],(4000,6000],(6000,8000],(8000,10000]五组,并作出如下频率分布直方图(图1):
(Ⅰ)试根据频率分布直方图估计小区每户居民的平均损失(同一组中的数据用该组区间的中点值作代表);
(Ⅱ)小明向班级同学发出倡议,为该小区居民捐款.现从损失超过6000元的居民中随机抽出2户进行捐款援助,求这两户在同一分组的概率;
(Ⅲ)台风后区委会号召小区居民为台风重灾区捐款,小明调查的50户居民捐款情况如下表,在图2表格空白处填写正确数字,并说明是否有95%以上的把握认为捐款数额多于或少于500元和自身经济损失是否到4000元有关?
附:临界值表参考公式:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,n=a+b+c+d.
 2015年7月9日21时15分,台风“莲花”在我国广东省陆丰市甲东镇沿海登陆,造成165.17万人受灾,5.6万人紧急转移安置,288间房屋倒塌,46.5千公顷农田受灾,直接经济损失12.99亿元.距离陆丰市222千米的梅州也受到了台风的影响,适逢暑假,小明调查了梅州某小区的50户居民由于台风造成的经济损失,将收集的数据分成[0,2000],(2000,4000],(4000,6000],(6000,8000],(8000,10000]五组,并作出如下频率分布直方图(图1):
2015年7月9日21时15分,台风“莲花”在我国广东省陆丰市甲东镇沿海登陆,造成165.17万人受灾,5.6万人紧急转移安置,288间房屋倒塌,46.5千公顷农田受灾,直接经济损失12.99亿元.距离陆丰市222千米的梅州也受到了台风的影响,适逢暑假,小明调查了梅州某小区的50户居民由于台风造成的经济损失,将收集的数据分成[0,2000],(2000,4000],(4000,6000],(6000,8000],(8000,10000]五组,并作出如下频率分布直方图(图1):(Ⅰ)试根据频率分布直方图估计小区每户居民的平均损失(同一组中的数据用该组区间的中点值作代表);
(Ⅱ)小明向班级同学发出倡议,为该小区居民捐款.现从损失超过6000元的居民中随机抽出2户进行捐款援助,求这两户在同一分组的概率;
(Ⅲ)台风后区委会号召小区居民为台风重灾区捐款,小明调查的50户居民捐款情况如下表,在图2表格空白处填写正确数字,并说明是否有95%以上的把握认为捐款数额多于或少于500元和自身经济损失是否到4000元有关?
| 经济损失不超过 4000元 | 经济损失超过 4000元 | 合计 | |
| 捐款超过 500元 | 30 | ||
| 捐款不超 过500元 | 6 | ||
| 合计 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
9.已知集合M={x|x>1},N={x|x2-2x≥0},则(∁RM)∩N=( )
| A. | (-∞,-2] | B. | (-∞,0] | C. | [0,1) | D. | [-2,0] |
19.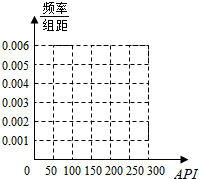 某城市随机抽取一年内100天的空气质量指数API的监测数据,结果统计如下:
某城市随机抽取一年内100天的空气质量指数API的监测数据,结果统计如下:
(I)求频率分布表中①、②位置相应的数据,并完成频率分布直方图;
(Ⅱ)请由频率分布直方图来估计这100天API的平均值;
(Ⅲ)假如企业每天由空气污染造成的经济损失S(单位:元)与空气质量指数API(记为ω)的关系式为
S=$\left\{\begin{array}{l}{0,0≤ω≤100}\\{4ω-400,00<ω≤200}\\{4.8ω-600,200<ω≤300}\end{array}\right.$,若将频率视为概率,在本年内随机抽取一天,试估计这天的经济损失S不
超过600元的概率.
 某城市随机抽取一年内100天的空气质量指数API的监测数据,结果统计如下:
某城市随机抽取一年内100天的空气质量指数API的监测数据,结果统计如下:| API | 空气质量 | 频数 | 频率 |
| [0,50] | 优 | 5 | 0.05 |
| [50,100] | 良 | ① | 0.2 |
| [100,150] | 轻度污染 | 25 | ② |
| [150,200] | 轻度污染 | 30 | 0.3 |
| [200,250] | 中度污染 | 10 | 0.1 |
| [250,300] | 中度重污染 | 10 | 0.1 |
| 合计 | 100 | 1.00 | |
(Ⅱ)请由频率分布直方图来估计这100天API的平均值;
(Ⅲ)假如企业每天由空气污染造成的经济损失S(单位:元)与空气质量指数API(记为ω)的关系式为
S=$\left\{\begin{array}{l}{0,0≤ω≤100}\\{4ω-400,00<ω≤200}\\{4.8ω-600,200<ω≤300}\end{array}\right.$,若将频率视为概率,在本年内随机抽取一天,试估计这天的经济损失S不
超过600元的概率.
6.设$M=\left\{{x\left|{y=\sqrt{x-1}}\right.}\right\}$,N={x|2x(x-2)<1},则M∩N为( )
| A. | {x|x≥1} | B. | {x|1≤x<2} | C. | {x|0<x≤1} | D. | {x|x≤1} |
3.已知存在实数α,使得关于x的不等式$\sqrt{x}+\sqrt{4-x}≥α$有解,则α的最大值为( )
| A. | 2 | B. | $2\sqrt{2}$ | C. | 4 | D. | 8 |